Graph Coloring

Problem 1

For these problems, the following graphs are given as examples

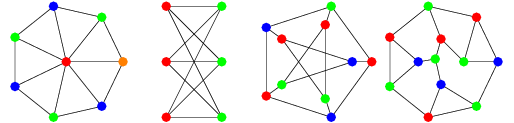
Part A

A graph is said to be two-colorable if it is possible to label the vertices with one of two colors so that no adjacent vertices have the same color. For example, the second graph above is two-colorable whereas the others are not two-colorable. Write the psuedocode for a function IsTwoColorable that returns true if a given graph is two-colorable, and returns false otherwise. Assume that the graph given is connected, i.e., there is a path between every pair of vertices.

Part B

Given your solution to Part A, describe how you would need to modify it to determine if the given graph was three-colorable. A graph is three-colorable if it is possible to label the vertices with any of three colors such that no adjacent vertices have the same color. Note, any graph that is two-colorable is three-colorable.

Problem 2

The data given below shows the steps necessary in the planning of a construction job. You should draw a graph that represents the dependencies between the various tasks and then attempt to answer the questions below.

Building a House (Cost of materials not in model)                                                   
  #            WaitOn     Task Name            hrs Labor Cost
  1                       Clear & Excavate      16    4000.00
  2            1          Foundation & Masonry  40    6400.00
  3            2          Framing & sub-floors  32    3840.00
  4            3          Sheathing             24    2880.00
  5            3          Roofing               24    4320.00
  6            4 5        Windows & Doors       20    2800.00
  7            6          Siding                24    2880.00
  8            7          Exterior Paint        20    2400.00
  9            3          Rough Plumbing        24    4800.00
 10            6          Rough Electric        36    7200.00
 11            6          Rough HVAC            40    8000.00
 12            9 10 11    Drywall               40    4800.00
 13            12         Attic Insulation      12    1440.00
 14            12         Hardwood Flooring     16    2560.00
 15            12         Finish Carpentry      40    6400.00
 16            12         Paint & Wallpaper     48    6720.00
 17            19         Carpets               16    1920.00
 18            16         Finish Electric       22    4400.00
 19            12         Finish Plumbing       26    5200.00
 20            12         Finish HVAC           28    5600.00
 21            12         Kitchen Carpentry     40    7200.00
 22            21         Appliances             6     960.00
 23            8 13 14 15 Punch List            24    4800.00
               17 18 19 20 /                  
               21 22      /                       
                                                    101520.00

For each of the problems below, give an algorithm for how to determine the answer. Then use the data above to test your algorithm.

• If everything goes according to plan, how long will it take?
• If we could cut the time in half by increasing the labor costs30%, where would that make sense?
• Would it be worth it if the cost of not being done was $1000 per day?
• Identify the critical path.