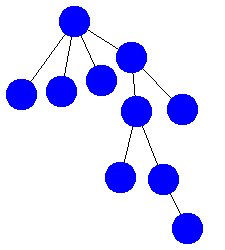
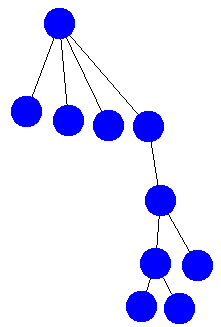
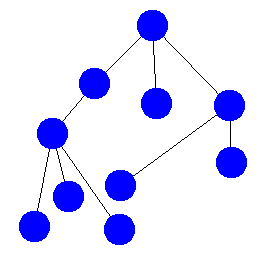
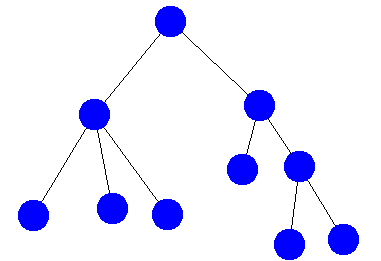
Tree 1
Two graphs A and B are isomorphic (i.e. equivalent) if you can find a one-to-one matching from the nodes in A to the nodes in B such that each pair of matched nodes has the same degree adjacency lists.
Two graphs are equivalent if you can answer "yes" to each of these question:
Consider the 5 trees below. Are the trees isomorphic? Group the trees into sets of trees that are isomorphic (i.e. trees in set A are isomorphic to other trees in set A, trees in B are isomorphic to other trees in B, but trees in A are not isomorphic to trees in B). You may want to use this graph creation tool to help you visualize and manipulate the trees.

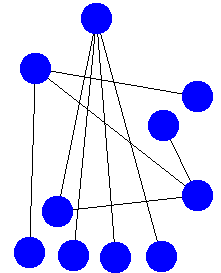
Consider facebook, an online directory that connects people.

Lets consider the connection by friends. On facebook, a friend is someone who mutually agrees with you that the two of you are friends. You are listed as one of their friends and they are listed as one of your friends.
Suppose we draw a graph in which each node in the graph is a person at Duke and each edge in the graph is a connection between two people at Duke who are friends (determined by facebook). If we could collect the data of everyone's list of friends at Duke, we could show a large graph of all the Duke friend connections. Our goal is to determine who is in the center of the graph, and to determine if the center person has the most friends or not.
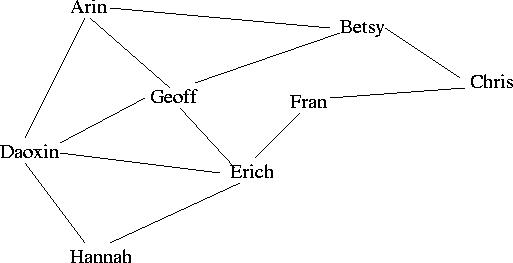
We will work with a much smaller graph to study this problem. Consider the following eight people and their friend connections.
In a graph the degree of a node is the number of edges attached to the node. When the graph represents the connections between friends, then the degree is the same as the number of friends.
For each person in the graph, determine their number of friends.
The shortest path distance between two nodes in a graph is the fewest number of edges one must walk along to get from one node to the next. For example, to get from Chris to Erich, there are several paths. One path goes through Betsy and then Geoff and is of length 3 (3 edges are traversed: Chris to Betsy, Betsy to Geoff, Geoff to Erich). There is a shorter path of length 2 through Fran (Chris to Fran, Fran to Erich). There are many more paths.
List the shortest path distance between every pair of names. The shortest path between a name and itself is zero and has been labeled for you.
| Names: | Arin | Betsy | Chris | Daoxin | Erich | Fran | Geoff | Hannah |
|---|---|---|---|---|---|---|---|---|
| Arin | .0 | . | . | . | . | . | . | . |
| Betsy | . | .0 | . | . | . | . | . | . |
| Chris | . | . | .0 | . | . | . | . | . |
| Daoxin | . | . | . | .0 | . | . | . | . |
| Erich | . | . | . | . | .0 | . | . | . |
| Fran | . | . | . | . | . | .0 | . | . |
| Geoff | . | . | . | . | . | . | .0 | . |
| Hannah | . | . | . | . | . | . | . | .0 |
Write an algorithm to find the shortest path from one node in a graph to all the other nodes. Assume there exists a path from that node to all the other nodes in the graph.
For each node in the graph above, calculate the sum of the shortest distances to all the other nodes in the graph. The node with the smallest sum is the center of the graph.
Which node is the center of the graph?
Does the center of the graph have the most friends (i.e. more than everybody else)?
Is the center of the graph always the person with the most friends? Draw a graph in which the center of the graph does not have the most friends. Your graph should have fewer than 12 nodes.
Consider the example graph below. Our goal is to find a path through the graph that visits every edge exactly once.
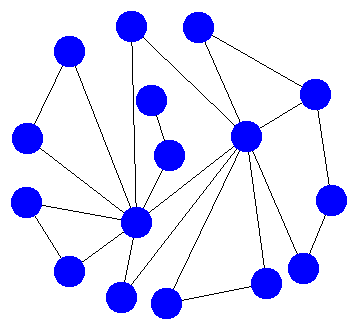
Question: How many nodes have an odd degree? How many have an even degree?
Question: Assume that a graph has at least 2 nodes with an odd degree. If you're going to have a path traversing every edge in the graph exactly once, can it start at a node with an even degree? Can the path end at a node with an odd degree? Explain.
Question: Are there any types of connected graphs for which it is impossible to find a single path visiting all edges exactly once? (Try stating a graph property making it impossible for such a path to exist.)
Question: Construct a path through this graph that visits every edge. Draw it out with arrows representing the direction you travel along each edge.
Now we'd like to have a general algorithm for finding such a path. This can be done by just making note of one simple fact: A path visiting all of the edges in a graph exactly once can only be found if the graph is connected.
Question: What algorithm would you propose for finding a single path through a graph that visits all edges in that graph exactly once?