Lecture 20: Analyzing Search Algorithms
- Starting on algorithms.
- Linear Search.
- Binary Search.
- The Logarithmic Function.
- Comparing Linear Search to Binary Search.
- O-notation and &Theta-notation.
What Is An Algorithm?
Throughout this class we've written some interesting programs. Believe it or not, each of those programs could be called an algorithm. This is using the term loosely, but basically an algorithm is just a step-by-step problem-solving procedure. Up until now, though, we haven't analyzed our programs much. We just wanted to know if the code worked and maybe if the code was easily understandable. As we'll start to see today, there are other ways we can analyze our "algorithms". The two metrics will focus on in this class are:
- Correctness: Does the algorithm correctly compute what it was supposed to compute.
- Efficiency: How fast does the algorithm run?
Efficiency is not really something we've cared about in our programs so far. Of course, the problems out programs have been solving haven't required great algorithmic solutions. It was the listeners and the graphical display errors that we had to worry about. So, let's look at something that isn't too hard to code, but could use a good algorithmic solution.
Searching For An Entry In An Array
You've worked with arrays quite a bit in this class. Sometimes we just had to traverse the array to deal with each element it held (like drawing each object in an array). Other times there may be a specific value within an array that we want to find. To simplify things, I'm just going to use an array that holds integer (int) values.
Let's say that I've got an array of int's, but that's all I know about it. I don't know how the values in the array may be ordered or anything else. If I need to search for the value "36" inside the array - to see if it's contained in one of the array entries - my options are very limited. The only choice I have is linear search: search through all of the elements in the list in some order. With an array of n items the easiest order to use is to start with entry 0 and continue looking until entry n-1. That's what the program LinearSearch.java does.
With this program we've got a true algorithm. We've got our problem - find an entry in an array if it exists - and a step-by-step procedure to solve it. It's important to separate our algorithm from its implementation.
- Algorithm:
- Start with the first entry in the data structure. Check every entry in increasing order to see if that entry contains the desired element. If the element is found, return
true. If the element is not found in every entry, return false.
- Implementation:
- Use a
for-loop to loop through all of the entries in the given array. The variable found begins with the value of false. Set the found variable to true if the entry is found. Return the value of the found variable after the for-loop is done.
Analyzing Linear Search
Since we've got an algorithm, the next step is to analyze it. First is the most important aspect of any algorithm: correctness. Is our algorithm correct? Well, our procedure is to start with the first entry in the array, then check every entry in increasing index order. This is guaranteed to check every entry in the array, so it's guaranteed to find the value we want if it's in one of those entries. Thus, our algorithm is correct. Now what about efficiency?
It's hard to tell exactly how fast my program will run? It seems to depend on how many entries the array has, how I wrote my code, how fast the computer running my code is... a lot of different factors. What's a good way to measure the efficiency of my code? The number of entries in the array is very important. That has to be included in our measurement. If the array has n entries we have to make n different steps to check each entry. The value of n could vary widely, so my measurement can't ignore it.
How about the code implementing my algorithm? In LinearSearch.java my for-loop just checks one condition for an if statement each time. On a given computer (with a given compiler for my code) this should take about the same amount of time for each iteration of the loop. Specifically, I can say that each iteration takes c1 time or less, where c1 is some constant amount in seconds, milliseconds, etc. What if the condition evaluated to true? Then I do a little more work to set the value of the found variable. Still, this only adds another constant amount of time, for a total of c2 time for that iteration. So, I can say that every iteration takes <= c2 time. That means the entire loop, which takes n iterations, will take <= c2n time.
Finally, what about the compiler and computer that compile and run my code? They make a difference, don't they? Sure, but for a given compiler and computer we're going to have a single constant for each iteration of that loop. Let's say that I use some value p to denote my compiler/computer pair. That means I can have some time constant cp to bound how long each iteration of my loop takes. So, on the compiler/computer pair p my algorithm would take <= cpn time to run. Got that? It's just two things:
- a constant for how long each iteration of the loop takes, and
- the number of iterations the loop makes.
An Alternative: Binary Search
Linear search was one algorithm I could use to look for an entry in an array. It worked if I didn't know the order of those entries, and it also works if I do know the order. Specifically, let's make things more interested by having the array entries be sorted in increasing order. So, the entry indexed by 0, would hold the smallest value of the array, the entry indexed at 1 would have the next smallest, etc. The largest value in the array would then be in the entry indexed by n-1, if there are n array entries.
With this array being sorted my linear search algorithm still works fine. However, now I can come up with an alternative: binary search. How does binary search work? A lot like you might search through a dictionary. Let's assume that all you know is that the dictionary entries are sorted in alphabetical order. How might you go about looking for the definition of the word "goal"? Here's one way: open up to the pages in the middle of the dictionary. If we find entries that come after "goal" in the alphabetical order, we search again on the front half of the book. If the entries we find come before "goal", we continue our search just on the back half of the book.
Here's a surprise: we just used another recursive algorithm. The first input to my recursive "method" was the entire dictionary. I then check the middle pages of the book to decide how to recurse. I then either recursively call my method on the front half of the book, or the back half of the book. This continues until I find a page containing the entry for "goal", or until I'm down to only a page or two and there's no room left to recurse. In the first case I return that I've found the desired entry, and in the second case I return that the entry isn't in the dictionary.
That dictionary search algorithm used binary search. Binary search works by continually dividing our search area in half until we either find our goal or get to the location where it would have to be and prove it's not there. The BinarySearch.java program implements this. Below are a few diagrams showing what happens when we search for the value "5". First, we've got the initial values for startIndex, endIndex, and middle.
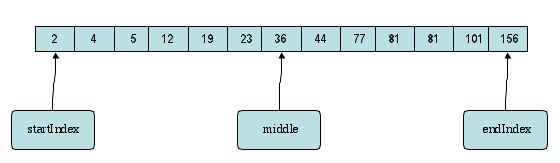
We check the middle entry and find that it's not what we're looking for. Moreover, the value we want is less than that found in the middle entry. So, we reset our endIndex variable.
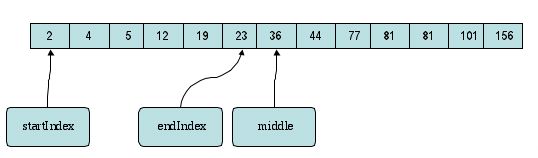
Now we can recurse on this new range. This range gives a new value for the "middle" variable.
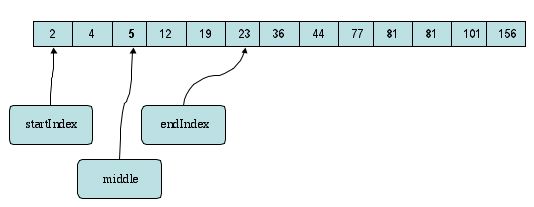
This entry turns out to contain the value we were looking for.
Analyzing Binary Search
The first thing to check about binary search is correctness. The way that we can do this is to maintain a loop invariant. Specifically, we'll ensure that for every call of our recursive method: if the desired value is in the array, its within the portion of the array that the recursive method is called on. Does our algorithm keep this loop invariant?
The first step of showing this is our base case: the first call to the binarySearch method. Here our range includes all of the entries in the array, so the desired element is either in this range or not in the array at all. What about later calls to the binarySearch method? Whenever we decrease the size of our range, we're taking a section above or below the "middle" entry we just checked. We know that the "middle" entry doesn't have what we're looking for, otherwise we would have returned. Also, we know that the number we're looking for can't be inside the range that we "exclude" because the if statement condition ensured that. Thus, we can conclude that the entry we're searching for can only be found in the remaining range - the range that we recursed on. This shows the correctness of Binary Search. Next lecture we'll analyze the running time of Binary Search as well.
Linear Search vs. Binary Search
Now that we've analyzed the
Last time we talked about two different ways to search: linear search and binary search. Here now are two applets for demonstrating those two different techniques.
Linear Search
Binary Search
Analyzing Binary Search
Our analysis for Binary Search starts out much that same as our analysis for Linear Search. Instead of iterations through a for-loop this time we've got recursive calls to the binarySearch method.
public static boolean binarySearch(int[] input, int startIndex, int endIndex, int goal){
System.out.println("Searching in the range: "+startIndex+" "+endIndex);
if(startIndex > endIndex)
return false;
int middle = (endIndex + startIndex)/2;
System.out.println(input[middle]);
if(input[middle] == goal)
return true;
else if(input[middle] < goal)
return binarySearch(input, middle+1, endIndex, goal);
else
return binarySearch(input, startIndex, middle-1, goal);
}
Except for the actual recursive call, everything that's done in this method can be bounded by a constant amount of time. (We can just assume that whatever time the recursive call takes is "assigned" to that call of the binarySearch method.) Thus, we get a constant bound of c3 for time taken on every call to the binary search method. This handles the constant factor, but how do I figure out how many times the binarySearch method is called in the worst possible case? It seems to divide the array in half each time it is called. Is there some way we can represent how many "halvings" it will take to eliminate the entire array?
In order to figure out how many "halvings" we need it can help to look at the opposite operation: doubling. Doubling is something that just seems more natural to a lot of people. If we figure out how many times we have to multiply by 2 to get to our array size that will also be how many times we have to halve it to eliminate the entire array.
| 20 | 1 |
| 21 | 2 |
| 22 | 4 |
| 23 | 8 |
| 24 | 16 |
| 25 | 32 |
| 26 | 64 |
| 27 | 128 |
| 28 | 256 |
| 29 | 512 |
| 210 | 1024 |
We can see that to get to our number of entries, 36, it will take 6 "doublings" to surpass that number. So, we can expect about 6 "halving" operations in the worst case to get from 36 possible array entries to just 1. Then, when we're left with just one possibility left, we can check it and then finish the algorithm.
The Logarithmic Function
The table above showed what powers of 2 we needed to get to various values. How do calculate what power of 2 is needed to get to a value we might have (like 36)? Luckily the logarithmic function does just what we need. If we take log2 36 we get a floating point value between 5 and 6. Since we can't make a fractional call to our method we just round up to 6 to figure out how many calls to our binarySearch method will occur in the worst case. This means that the running time of our binary search method can now be bounded by c3log2(n). Again, n is the number of entries we're searching through and c3 is our constant time bound on each call to the binarySearch method.
In computer science everything is done in binary and the trick of "halving" used by binary search shows up in many other algorithms. Using the log2 function is quite common. Thus, the usual notation in computer science is lg to represent log2. Using this, we can rewrite our running time for the binary search method as c3lg(n). Here's a table showing the running times of each search algorithm for increasing values of n.
Comparing Linear Search vs. Binary Search
Now that we've analyzed the running time for binary search we can compare it to linear search. To fully account for everything, I should write the running time of binary search as c3lg(n) + c4. This extra constant c4 is just to account for whatever constant amount of time was spent before the first call to the binarySearch method. Similarly, the running time for linear search gets an extra constant added on: c1n + c2.
To show off the difference that the lg function makes, the table below compares the values of n and lg(n) for various values of n. I also give the full functions for linear search and binary search at the top, but the constants are left off for the table entries to save space.
| Values of n | Linear Search | Binary Search |
| n |
c1n + c2 |
c3lg(n) + c4 |
| 100 | 100 | 7 |
| 1,000 | 1000 | 10 |
| 1,000,000 | 1,000,000 | 20 |
| 1,000,000,000 | 1,000,000,000 | 30 |
| 1,000,000,000,000 | 1,000,000,000,000 | 40 |
| 1 x 1015 | 1 x 1015 | 50 |
These values for lg(n) are rounded up to the closest integer, but this table is sufficient to show the immense difference that the lg(n) function makes. I left off the constant factors in that table, but would they matter? The c2 and c4 terms were justed added on and weren't changed by different values of n. However large those values might be, they're still constants. That means there's some point where the value of n can become so large that those constant become tiny, tiny low-order digits.
What about the c1 and c3 terms? They were actually multiplied against the functions of n. Still, they're just constants. As the table above demonstrates, multiplying lg(n) by a constant factor isn't going to matter. At some point n becomes large enough that binary search's function is going to give much smaller values than linear search's function. This occurs because the function lg(n) grows much more slowly than the function n. This was really the only important part of each algorithm's function when we let n grow large. Computer science recognizes this and even has special notation for comparing such functions.
O-Notation and &Theta-Notation
For the two search algorithms I analyzed above I was focusing on the worst possible cases. In keeping with this focus, my functions were designed to give an upper bound on how long each algorithm could take on a given input size of n. For the linear search algorithm I bounded it's running time with the function: c1n + c2. Recall that the constant factors didn't make much difference when we allowed the value of n to grow. So, in computer science we would say that the running time of linear search is O(n). This notation would be pronounced as big-Oh of n or Oh of n. It strips away the constant factors that didn't make much of a difference and focuses on just the important terms.
Similarly, for the binary search algorithm we would give it's running time as O(lg n). This notation is common for stating the running times for algorithms. What does the notation mean exactly? It describes the asymptotic upper bound for the magnitude of a function in terms of a simpler function. In this case we were describing the complicated functions with the constant factors with simpler functions that dropped those constant factors. But what's an asymptotic upper bound? It's a bound on how the function behaves as it's variable (in our case, n) grows towards infinity. The picture below gives such an example.
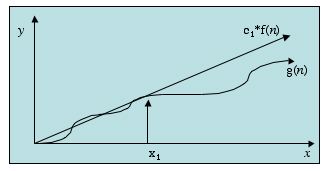
In this picture we've got a function g(n) that is asymptotically bounded by f(n). For some constant factor c1 multiplied against f(n), after a certain point x1 the g(n) function will always be equal to or below the c1f(n) function. Thus, we could say that g(n) is O(f(n).
Very similar to O-notation is &Theta-notation. The picture below shows an example, again with g(n) being bounded by f(n).
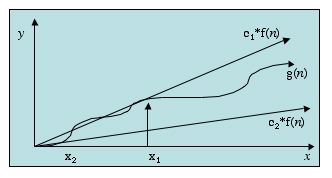
In this case we've got two different constant factors: c1 and c2. The first one allows f(n) to serve as an upper bound for g(n) after the point x1. The second constant c2 allows f(n) to serve as a lower bound for g(n) after the point x2. In this particular example f(n) grows so much like g(n) grows that f(n) can bound g(n) both above and below. This means that, asymptotically, f(n) gives a pretty good approximation for g(n). Therefore, we can say that g(n) is &Theta(f(n)).





