
In previous lectures we introduced the idea of determining the asymptotic running time of an algorithm. Basically, once we start getting into very large inputs sizes, how fast will this algorithm run. Given an input with n items, some algorithms we've seen ran in time on the order of log(n) many steps (binary search), in n steps (linear search), n*log(n) many steps (merge sort), and in n2 many steps (selection sort). Merge sort was the method that broke the problem up into subproblems, sorted those, then merged those answers back together. Selection sort kept finding the next smallest number in the unsorted pile and adding it to the end of the growing sorted pile. To better illustrate these differences I've created a program to compare some example running times.

In the entries printed out above a program calculated values given different input sizes for n: from 10 up to 1,000,000,000 (one billion). In the first set of printed values we just have the numbers given by the various functions of n. In the second set, we try to make sense of those numbers by giving speeds to some computer processors running those programs. The first processor running binary search will take 1 minute for each execution step. The second processor, running linear search, will take 1/100 of a second. The third computer running merge sort will take 1/1,000 of a second per step. Finally, the fourth comptuer running selection sort takes a quick 1/1,000,000 of a second per step.
For small input sizes the faster processors obviously have the advantage. Yet, for small input sizes all of the algorithms are fast so it really doesn't matter. We care about when any of the algorithms start running slowly and this happens when we get to large input sizes. Regardless of input sizes, binary search is running quickly. It still only takes about 21 minutes when we get up to an input size of one billion, and that's at about 1 minute per execution step!
On the other end of the spectrum is selection sort running on the order of n2 steps based on the input size of n. Even running at about 1,000,000 execution steps per second, it's going to take over 11 days to sort those entries. Merge sort, on the other hand, is going to take about 0.16 days or less than 4 hours. When we get up to a billion input entries the disparity is much more glaring. Binary search takes only 21 minutes (at one step per minute), linear search takes about 116 days (at 100 steps per second), merge sort takes about 240 days (at 1000 steps per second) and selection sort takes... well, over 30,000 years. Even with a much faster processor selection sort is going to take a lot longer to complete its task.
While selection sort took a while to solve for very large inputs, we do find that it runs quickly when given a reasonable input of a million entries or less. That's especially true when you consider that your computer runs on the order of a billion execution steps per second (Gigahertz) rather than a million steps per second (Megahertz) that was uses for the example above. An problem whose running time can be written as a polynomial expression of the input size (i.e. n3, log(n), etc.) are known as tractable problems. Yet, there are some problems that we have no fast algorithm to solve and, for inputs of just 100 or 1000 entries, we have no way to really solve the problem (using any computer). We have algorithms that will solve it... they'll just take longer to execute than the expected life time of our solar system's Sun! These types of problems are known as intractable problems.
To get a glimpse of this, I've added one more entry to the table of values below. Now instead of a running time of taking n2 steps, given an input size of n, what if those were reversed? What if we took on the order of 2n steps, given the input size? Well, an example problem that might take this many steps involves those truth tables you worked with earlier for boolean logic. What if I gave you a boolean expression, using n different variables, and asked you to find some setting of the variables being true or false that would make the total statement true. ...or return that there is no such assignment. For small statements, that's easy to do:
A*!B*C
For the statement above we could try various settings of the variables to true or false and eventually find a setting that worked. In this case setting A = true, B=false, C=true is the only way to make the overall statement be true. Remember that because each variable has 2 possible settings, with each new variable we double the possible truth setting combinations. So, to try all of the possible truth settings in our truth table, for n variables we have 2n settings to try. Is this bad? Check out the numbers below.

We see that the variables in this Java program very quickly run out of room (I was using a double variable to avoid overflow) and just start saying "Infinity". Here's a closer look at the extremely fast growth of this function:
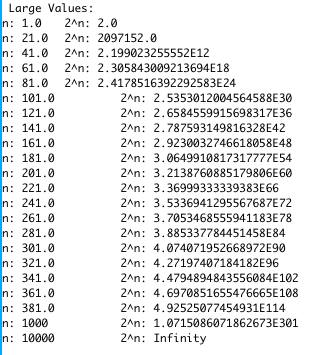
The table above is really just an extension of the powers of 2 tables that we saw in earlier lectures. As we can see from those tables or from the one above, a problem size of even 60 or 100 variables is too large to be computed. Yet, 100 or even 1000 entries doesn't seem unreasonable for an input size to a problem we care about.
While finding ways to make boolean statements evaluate to true actually can have a lot of uses, they may not be easy to see initially. For a more common example of an intractable problem we use the Traveling Salesman Problem. In this problem you've got some set of cities that you need to visit. You start in one city, visit all of the others, then return back to the city you originally started from. This problem might come up for a sales representative of a company needing to arrange and travel to meetings in other cities. In that case you'd like to reduce travel time and cost from fuel and other expenses. The same could be true of the task of delivering mail, shipping packages, or simply planning a vacation!
So, how do you plan the shortest route or tour visiting all cities from an input size of n. The easiest algorithm you might think of would be to try all possible orders in which you could visit the cities. The problem is that for n cities there are n! possible orderings! In our textbook in chapter 13 the write a program for trying all possible orderings and, based on how fast that program ran, make estimates on how long it would take for larger input sizes. For 10 inputs: about 4.64 hours. For 14 inputs: 12.71 years. For 20 inputs: 354,875,356 years!
Could a faster computer make a difference? Yes, but not a big difference. Imagine that we could build a computer 1,000,000 (a million) times faster than the computer our textbook used for their trial run. The program would still take over 354 years. And remember that with each added input our running time will double. So, even if you could run the program fast enough to solve a case with 20 inputs in only 1 second, bumping the input size to 40 inputs will put you right back at a running time of a few hundred million years (since 40 inputs would be 20 more than 20 inputs, and 20 inputs originally took a few hundred million years). So, a faster computer simply isn't the answer here. We either need a completely different way of processing, or a much better algorithm. Unfortunately, while there are algorithms to improve on our naive "try all possibilities" approach, there's nothing that gets this problem off the list of intractable problems.
The traveling salesman problem is one of many problems referred to as NP-complete problems. Every problem in this group is intractable: basically meaning it can't be quickly solved with any algorithm that we currently know. The problems in this category are interesting for a number of reasons, but especially because (1) many are key problems regularly faced by businesses or individuals and (2) if you could solve any problem in the group quickly, that algorithm could be used to quickly solve any other problem in the group.
So, not only are many NP-complete problems important to want people are needing to solve, but they're all related to each other. This is because, while computer scientists haven't been able to find a fast algorithm for any of these problems, they have devised fast algorithm for turning one NP-complete problem into another. This, in a sense, is translating one problem into an instance of a different problem type: such as if you were to somehow decribe the traveling salesman problem as a boolean expression that you needed to somehow resolve to true (and that translation can be done). So, if a fast algorithm is every found for any of the NP-complete problems the all of the other problems can just be translated to that solved NP-complete problem. Then everything can be solved using that single, fast algorithm. Unfortunately, researchers have tried for decades without any success (and the immense reward for finding a fast algorithm did inspire a lot of effort on the part of a lot of researchers). So, by now the research community tends to think that no fast algorithm exists and that we simply haven't been able to prove that yet.
The algorithms that we've been considering so far using a single processor. What if we had several processors or several computers working together? For the case of the traveling salesman problem this could be a big help. Our algorithm before was to simply check all possible orderings for visiting cities and then see which had the shortest path. If we have two computers then we can give half of the possible orderings to one comptuer and the other half to the other computer. Then it's just a matter of comparing the "best" answer that each computer found and taking the best out of those two answers. In this way having 2 processors cuts the time to execute our algorithm in half. So, when new computers talk about having "dual cores" or two or more processors in a single computer, this ability to divide up the workload is the benefit your getting.
Still, we can see that having a couple more processors isn't going to solve any of the NP-complete problems. For the case of statements of boolean variables, each new variable doubled the number of truth settings that we would have to try. If we have p processors then adding one more to get p+1 processors can help, but it doesn't always reduce the workload by half. Also, getting something like 2n processors is out of the question for any value of n that we couldn't already solve. So, parallel processing can certainly improve our running time, but it doesn't solve all of our problems.