HOMEWORK 3

Background: Ch. 1.2, 1.3, 8.1, 8.2.

Due September 24th:

• 3.1: Low values of the insertion index are very common in practical applications. In class, we showed that insertion sort takes O(kn) time on lists with insertion index k. Show that it can actually run even faster. In particular, give a list with insertion index k=n/2 for which insertion sort takes $\Theta(n)$.

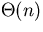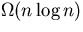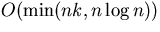• 3.2: (a) Say why mergesort can take $\Omega(n \log n)$ even for insertion index k=1. (b) What simple change can we make to mergesort to help? (c) Analyze the effect of this improvement for k=1. (d) Extend your argument to arbitrary k to get a $O(\min(nk, n\log n))$ bound for mergesort. [Part (d) is extra credit.]

• 3.3: In most randomized models of computation, there is a primitive operation RANDBIT that returns 0 with probability 1/2 and 1 with probability 1/2. (a) Taking RANDBIT to be a unit-time primitive, design a randomized algorithm RANDTRIT that returns 0 with probability 1/3, 1 with probability 1/3, and 2 with probability 1/3. (b) Compute the expected number of calls to RANDBIT that your algorithm makes. (c) Give a worst-case bound.

• 3.4: CLR Exercise 8.2-1 (pg. 160).

• 3.5: The quicksort vs. insertion sort comparison we ran was on random lists. Rerun the experiment on sorted lists and plot the data. Compare randomized quicksort, ``pivot on first'' quicksort, and insertion sort.

• 3.6: Below is code for the ``merge'' part of merge sort, defined on lists of arbitrary size. Analyze the function using the potential function method. Assume that A and B are ended by the symbol ``EOF'' and that C is sufficiently large to support all the elements of A and B.

  int merge( vector<int> & A, vector<int> & B, vector<int> & C)
  {
  
    int i = 0;
    int j = 0;
    int k = 0;
    
    while( true )
    {
      if ( (A[i] == EOF) && (B[j] == EOF) )
        return;
  
      if ( (B[j] == EOF) || (A[i] <= B[j]) )
      {
        C[k] = A[i];
        i++;
        k++;
      } else
      {
        C[k] = B[j];
        j++;
        k++;
      }
    }
  }
  

• 3.7: Assume you have a unit-time subroutine rand(k) that returns a number between and k-1 from the uniform probability distribution. Explain how to generate a uniform random permutation of the numbers through n-1 in 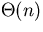$\Theta(n)$. [Extra Credit.]