


Next: HOMEWORK 6
Up: CPS 130 Homeworks
Previous: HOMEWORK 4
Background: Ch. 7, Ch. 13.1, 13.2, 13.3.
Due October 15th:
- 5.1: We've got an array A with n elements in it. Someone
gives us a number k<n (think relatively big for n, relatively
small for k). We want an algorithm that finds the largest k
elements in A fast. Give big-O running times in simplest form for
each of these algorithms. (a) Sort all the elements, read off the
largest k. (b) Build a heap out of the entire set, call ``extract
max'' k times. (c) Use select to find the element with rank n-k,
find the k largest elements, sort them. (d) Insert all the elements
into a splay tree, then find max, and find predecessor (opposite of
successor) k times.
- 5.2: CLR Exercise 7.5-5 (pg. 151).
- 5.3: Give worst-case bounds for executing find min, find max, find
min, find max, find min, find max, ... k times on (a) balanced
binary search tree, (b) an unbalanced binary search tree, and (c) a
splay tree. (d) Which is asymptotically most efficient if
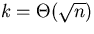 ?
?
- 5.4: We've got n numbers stored in a heap. We want to find the
kth largest number (where the first largest number is at the root).
For simplicity, assume there are no ties in the set of keys. Explain
how to do this in
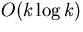 time (i.e., independent of n).
[Extra credit.]
time (i.e., independent of n).
[Extra credit.]



Next: HOMEWORK 6
Up: CPS 130 Homeworks
Previous: HOMEWORK 4
Michael Littman
12/4/1998