Theorem: For an integer a>1, we can divide a by two (and
round down) 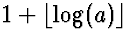 times before we get down to
zero.
times before we get down to
zero.
Proof: For a>1, let T(a) be the number of times we can divide
a by 2 (and round down) before we get down to zero.
We can express T recursively as: T(1) = 1, and for a>1,
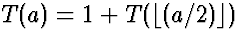 .
.
We want to show that 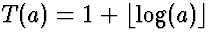 .
.
- Base Case: a=1.
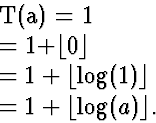
Correct.
- Next, note that any number greater than one, divided by 2 and
rounded down gives a result strictly less than the original number and
greater than or equal to one. (You could prove this by induction,
too.)
- Inductive step: Assume that for all a' < a, the theorem holds.
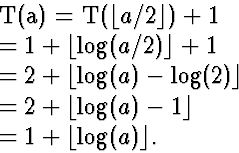 Correct!
Correct!
- QED.



Next: About Proofs
Up: RECURSION
Previous: A Recurrence Relation
![]() times before we get down to
zero.
times before we get down to
zero.
![]() .
.![]() .
.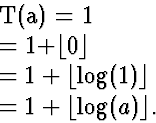
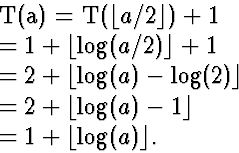 Correct!
Correct!