Divide and Conquer

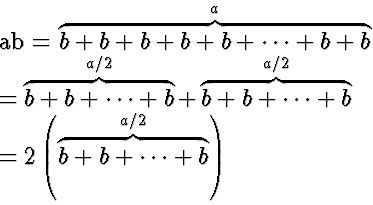
When a is even...

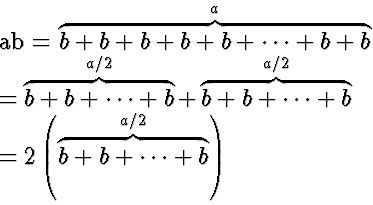
$\begin{eqnarraystar} ab &=& \overbrace{b+ b+ b+ b+ b+ \cdots+ b+ b}^{a} \ &=& ... ...^{a/2}\ &=& 2 \left(\overbrace{b+ b+ \cdots+ b}^{a/2}\right)\end{eqnarraystar}$

When a is odd...

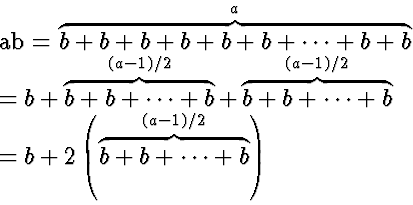
$\begin{eqnarraystar} ab &=& \overbrace{b+b+b+ b+ b+ b+ \cdots+ b+ b}^{a} \ &=&... ...\ &=& b+2 \left(\overbrace{b+ b+ \cdots+ b}^{(a-1)/2}\right)\end{eqnarraystar}$

We solve the problem by breaking it into roughly equal-size subproblems, solving them separately, then combining the results (in this case, there's just one subproblem).

Rule #2 of Good Algorithm Design: Divide-and-Conquer!

Next: Analysis Up: RECURSION Previous: Exponentiation