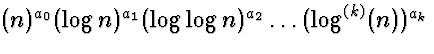
This is not standard, but I think you might find it useful.
Many of the most important functions are asymptotically equivalent to a function that can be specified in the following ``normal'' form:
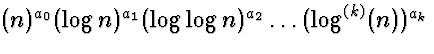
where ![]() for all
for all ![]() , and ak > 0.
, and ak > 0.
Any function that combines addition, multiplication, logarithm, maximization, or minimization of this type of function can be reduced to this form. Ought to be able to handle division also.
Scalar Multiplication Rule: As an easy starting point, any
positive leading multiplicative constants can be dropped: ![]() .
.