No matter how we sort, if we plan to put n items in order, we
need to compare a sufficient number of items to uniquely identify the
permutation.
- So, how many different permutations are there?
- Each comparison has the effect of ruling out some of the
permutations. So, we can imagine that we start out with all
permutations being possible, then making a comparison and splitting
the set of possibilities in two.
- The entire sequence of comparisons for any given sorting algorithm
can be thought of as a big tree, where each leaf of the tree contains
no more than one permutation.
- The deepest path in this tree is the maximum number of comparisons
we need to do to sort any list. We'll show that this is
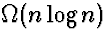 .
.



Next: The Bound
Up: SORTING IN LINEAR TIME
Previous: A Lower Bound