Vectors and Matrix-Vector Product

A vector is just a 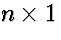$n \times 1$ matrix.

The product of an 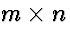$m\times n$ matrix A and an 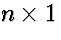$n \times 1$ vector x is an 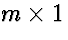$m \times 1$ vector y where $y_i = \sum_{j=1}^n A[i,j] x[j]$. It is the ``dot product'' between the rows of A and x.

Matrix-vector products come up all over the place. For example:

• If A is the matrix of student exam grades and x is a vector of ``weights'' (what fraction of the final grade is assigned to each exam), then A x is a vector of final scores for each student.
• If A[i,j] is the number of times word j appears in article i and x[j] is 1 if and only if a ``query'' contains term j, then A x is a vector with one entry per article with the total number of query terms appearing in that article.