Using the Inequality

For the type of analysis we're talking about today, we insist that $\hat{c}_i = 0$, and $\Phi(D_k) = 0$. Using the fundamental inequality, we get:

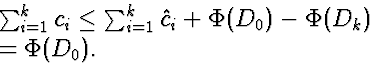
\begin{eqnarraystar} \sum_{i=1}^k c_i &\le& \sum_{i=1}^k \hat{c}_i + \Phi(D_0) - \Phi(D_k)\ &=& \Phi(D_0).\end{eqnarraystar}

Thus, the maximum value of the potential function gives a worst-case bound on total running time.

The potential function measures the work it will take to solve the problem.

next up previous
Next: Analysis of Permutation Problem Up: POTENTIAL FUNCTION ANALYSIS Previous: Fundamental Potential Function Inequality