Complete Binary Search Tree

Given a list of numbers, we could create a well-balanced binary search tree.

• Sort A.
• Pick i as the appropriate halfway point. Let i be the root.
• Make a complete binary search tree out of A[1] through A[i-1] and make it the left subtree. Do the same with A[i+1] through A[n] and make it the right subtree.

If we choose i to be 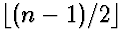$\lfloor (n-1)/2 \rfloor$, what is the height of the tree? How prove?

Running time?

How can we choose i so that the resulting tree is complete (i.e., deepest level is ``left justified'')?