Propose to shift the pattern to the right by the least amount that guarantees not to skip any occurrence of the good-suffix already matched.
T = abbbaabab
||
P = cabaab
P = cabaab
![]() .
In example above, j = 4, want maximum k such that
.
In example above, j = 4, want maximum k such that
![]() .
.
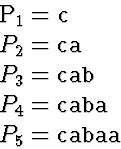
So, ![]() .
.