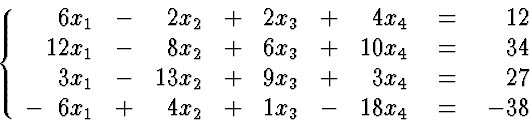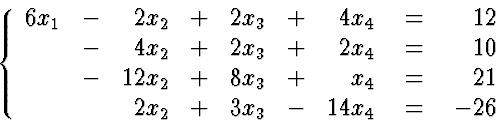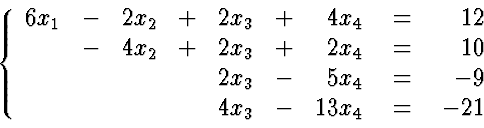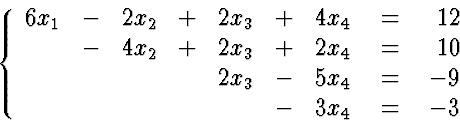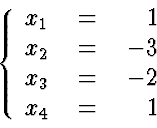Basic form: 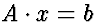 .
.
An example:
![\begin{displaymath}
A = \left[\begin{array}
{cccc} 6 & -2 & 2 & 4 \
12 & -8 ...
...0 \ 3 & -13 & 9 & 3 \ -6 & 4 & 1 & -18 \end{array} \right],\end{displaymath}](img41.gif)
![\begin{displaymath}
x = \left[\begin{array}
{c} x_1 \ x_2 \ x_3 \ x_4 \end{array} \right],\end{displaymath}](img42.gif)
![\begin{displaymath}
b = \left[\begin{array}
{c} 12 \ 34 \ 27 \ -38 \end{array} \right].\end{displaymath}](img43.gif)
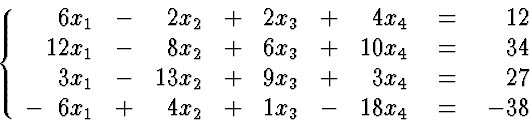
- 1.
- Eliminate x1 in equations 2,3 and 4
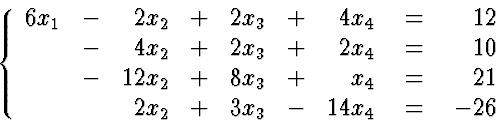
- 2.
- Eliminate x2 in equations 3 and 4
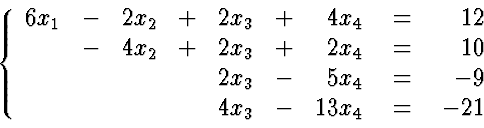
- 3.
- Eliminate x3 in equation 4
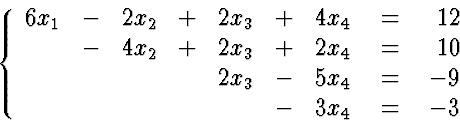
- 4.
- Solve the above system starting from the last equation
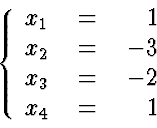



Next: Expressing the Algorithm
Up: SOLVING LINEAR SYSTEMS
Previous: SOLVING LINEAR SYSTEMS
![]() .
.![\begin{displaymath}
A = \left[\begin{array}
{cccc} 6 & -2 & 2 & 4 \
12 & -8 ...
...0 \ 3 & -13 & 9 & 3 \ -6 & 4 & 1 & -18 \end{array} \right],\end{displaymath}](img41.gif)
![\begin{displaymath}
x = \left[\begin{array}
{c} x_1 \ x_2 \ x_3 \ x_4 \end{array} \right],\end{displaymath}](img42.gif)
![\begin{displaymath}
b = \left[\begin{array}
{c} 12 \ 34 \ 27 \ -38 \end{array} \right].\end{displaymath}](img43.gif)