Least Squares

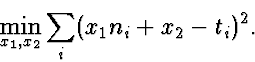
So, what solution do we pick? A classic example is to find the x₁ and x₂ that give the best values in a ``least squares'' sense:

$$\min_{x_1,x_2} \sum_i (x_1 n_i + x_2 - t_i)^2.$$

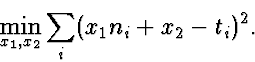
This scoring scheme is reasonable because it is optimized for a perfect fit, and the worse the predictions, the worse the score.

Note: You can think of this as being a generalization of the notion of an average. Recall that $\min_{x_1} \sum_i (x_1 - t_i)^2 = \sum_i t_i / n.$