For all matrices 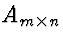 ,
, 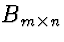 and
scalars c:
and
scalars c:
- c(A+B)=cA+cB
- A+B=B+A
- (AT)T = A
- A-A=0
- (A+B)T = AT+BT
In addition, for all matrices 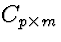 :
:
- (AB)T = BT AT
- C(A+B) = CA + CB
However, 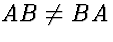 in general (even if both are square):
in general (even if both are square):
![\begin{displaymath}
\left[\begin{array}
{cc} 1 & 2 \ 3 & 4 \end{array} \right]...
...left[\begin{array}
{cc} 10 & 4 \ 24 & 10 \end{array} \right],\end{displaymath}](img36.gif)
but
![\begin{displaymath}
\left[\begin{array}
{cc} 4 & 2 \ 3 & 1 \end{array} \right]...
...left[\begin{array}
{cc} 10 & 16 \ 6 & 10 \end{array} \right].\end{displaymath}](img37.gif)



Next: Solving Equations
Up: MATRICES AND VECTORS
Previous: Matrix Multiplication
![]() ,
, ![]() and
scalars c:
and
scalars c:
![]() :
:![]() in general (even if both are square):
in general (even if both are square):
![\begin{displaymath}
\left[\begin{array}
{cc} 1 & 2 \ 3 & 4 \end{array} \right]...
...left[\begin{array}
{cc} 10 & 4 \ 24 & 10 \end{array} \right],\end{displaymath}](img36.gif)
![\begin{displaymath}
\left[\begin{array}
{cc} 4 & 2 \ 3 & 1 \end{array} \right]...
...left[\begin{array}
{cc} 10 & 16 \ 6 & 10 \end{array} \right].\end{displaymath}](img37.gif)