Potential Function Analysis

Intuition is that all the work happens in calls to Visit and there can't be too many such calls because nodes and edges are turning from white to gray to black.

• Operation is a call to Visit.
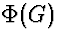• $\Phi(G)$ is the total number of white edges in G:

  $$\sum_{u\in V} \chi(G[\mbox{start},u]=\mbox{\sc white})+ \sum_{v\in\mbox{\em Adj}[u]} \chi(G[u,v]=\mbox{\sc white}).$$

• Each time we enter Visit, an edge becomes black, decreasing the potential function by one and ``paying for'' the non-recursive work in the subroutine. How do we know that an edge isn't turned black twice?

• Maximum value of the potential function is one contribution from each edge and one from each node (because of ``start''). So, running time is: O(n+m).