Planning with Probabilities

Probabilistic vacuum: dirt is removed with probability $\Pr(0.8)$.

What's the probability a square would be still be dirty after 10 sucks, given that it begins dirty?

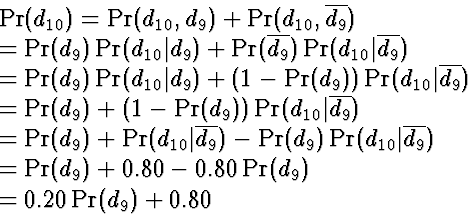
\begin{eqnarraystar} \Pr(d_{10}) & = & \Pr(d_{10}, d_9) + \Pr(d_{10}, \overline... ...r(d_9) + 0.80 - 0.80 \Pr({d_9}) \\ & = & 0.20 \Pr(d_9) + 0.80\end{eqnarraystar}

We are assuming that dirtiness now next conditionally dependent only on dirtiness now: Markov property.

How solve?

next up previous
Next: Reasoning with Probabilities Up: PREVIEW Previous: PREVIEW