Lab 7: Sierpinski Fractals and Recursion

2 iterations	3 iterations	4 iterations	5 iterations

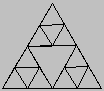
It may not be obvious from these illustrations that inside each larger triangle, three (not one) smaller triangles are drawn. For instance, in the diagram labeled "2 iterations," one smaller triangle has been drawn in each corner of the larger triangle; the smaller triangle that appears in the middle is purely the result of the other three having been drawn.

The Algorithm

In this lab you will be creating the Sierpinski fractal which you may have already seen in class. The algorithm for creating the pattern is very simple:

1. Draw an equilateral triangle using points x, y, and z
2. Create three more Sierpinski fractals, each with the following vertices
   • x, midpoint(x,y), midpoint(x,z)
   • y, midpoint(y,x), midpoint(y,z)
   • z, midpoint(z,x), midpoint(z,y)

As you might notice, the algorithm is infinite recursion. It is recursive because the algorithm for drawing a Sierpinski fractal includes drawing another Sierpinski fractal. The algorithm is infinite because there is no way to draw a final figure (there is no base case). In theory fractals are infinitely recursive, but in practice the recursion continues only a set number of steps, or until further recursion does not noticably change the image. In our case, the algorithm is very similar to the theoretical algorithm:

  void triangle(Point x, Point y, Point z)

1. Draw a triangle using points x, y, and z
2. If number of steps is greater than  zero
   then reduce the number of steps and create three more Sierpinski fractals, each with the following vertices
   • x, midpoint(x,y), midpoint(x,z)
   • y, midpoint(y,x), midpoint(y,z)
   • z, midpoint(z,x), midpoint(z,y)

Try to use the algorithm to draw on paper a third generation Sierpinski fractal. Yours should look like the one above and the ones done in class. If you can't draw it at this point, it might be a good idea to reread the algorithm or ask a TA to help explain it. You can also try out the demo to help you understand the algorithm.

Point: A Point is a Java class that stores an x and a y value (a coordinate pair). For example:

Point p1,p2,p3;
p1 = new Point(5,6);
p2 = new Point(10,20);
p3 = p1;

p1.x = 10;
p3.y = p1.y/2;
z = p2.x;

The Implementation

You need to copy the following code, and complete it: http://www.duke.edu/~gcl4/Sierpinsky.java

You will need to write two methods:

• public void triangle(Point p0, Point p1, Point p2, int numTimes)

  This is the recursive function that actually draws the triangles on the screen. The first thing you should check is to see if the number of steps is greater than zero. If so, then:

  1. Find the three midpoints (three lines)
  2. Recusively call the triangle function 3 times making sure to reduce numTimes by 1 (three lines)
  3. Draw the triangle, using the drawTriangle method given to you

• public actionPerformed (actionEvent event)

  In this method, the only action you need to perform is if the draw fractal button has been pressed. In this case,

  1. Clear the screen (use the DrawingPad clear() method).
  2. Create three Points (use your prelab)
  3. Get the number of generations from the IntField
  4. Call the triangle method that you have created