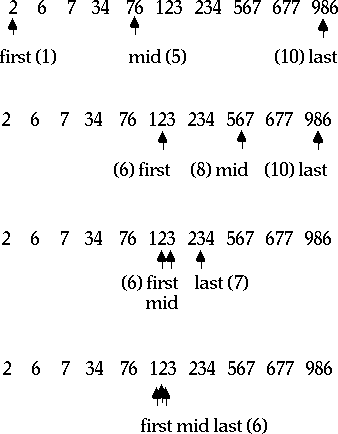
Binary search is the algorithm we discussed in class for finding names in a phone book. The picture below describes graphically searching for the number 123:
Assume we have a phone book (sorted by last name) with 4 entries, what is the maximum number of comparisons one must do to find a the entry for Jeff Forbes using binary search? (1 point)
solution:
for purposes of illustration let us call our 4 entries " Jeff Forbes", "Owen Astrachan", "Susan Rodger", and "Robert Duval".
Since the names are sorted by last name we consider only their last names.
our search will look as follows
Astrachan .................... Duval...............Forbes.............Rodger
after one round of search (1 comparison) we are left with
Forbes...............Rodger
after another round of search (1 comparison) we have
Forbes
hence we have found our entry for Jeff Forbes after 2 comparisons
we can note that for 4 = 2^2 we had 2 comparisons
What is the maximum number of comparisons if we have to search through 512 entries in the phone book using binary search? (2 points)
we can note that 512 = 2^9. This means if we divide 512 in half 9 times we have 1 element left. Therefore we need 9 comparisons to perform our search on a 512 element phone book.
Name a type of business that will not by affected by the WWW in the coming years. Justify your answer briefly.(1 point)
Write the HTML code for a link to the page at http://www.nj.com with the text New Jersey Online. (2 points)
"<A HREF: "http://www.nj.com" >New Jersey Online</A>"......(without the quotes) NB: html tags are case insenstive so HREF = href
Java is designed to run on many different kinds of computer systems. ( True / False )? (1 point)
TRUE
The following is an example of a Java variable declaration. ( True / False )? (1 point)
jack = new TextField("Hello World.");
False. This is an example of Java object creation.
Name some programming languages? (1 point/4 langs., 2points/8 langs.)
C, C++, Basic, Visual Basic, Fortran, Cobol, Lisp, Pascal, ML, C#, Smalltalk, Ada, APL, PL-1, Shell, etc...
Give a winning strategy for the following game: (1 point)
You and a friend have a stack of 10 coins.
One each person's turn, he or she removes either 1 or 2 coins from the stack.
The person who removes the last coin wins.
Consider the simplest case when both players must play i.e when there are 3 coins left. Since the max number of coins the palyer whose turns it is can pick up is 2, that player loses. We see that if it is a players turn when there are 3 coins, that player is in a position of weakness. We extropolate this idea to 4 coins. Again, we see by picking one coin, we can force the opponent to be in the "3-coin" unfavorable position. The 5 coins state is similar to 4 so we consider the 6 coin state. We see that a player playing when there are 6 coins is in the unfortunate position of being put in the unfavorable "3 coin state" regardless of how he/she plays. We further see that this is true for ANY multiple of 3 .
Our strategy therefore would be to be ensure the opponent always plays when the number of coins is a multiple of 3, guarranteeing that the opponent will find themseleves in the losing "3 coins state" at the end of the game .
End of quiz