Many living things grow in such a way as to produce fractal patterns. Examples include the passageways in the lungs or the branches of a tree. In these cases the self-similarity on different scales arises because growth involves repetition of the same simple process (e.g. branching). These simple, repetitive processes can often be neatly summarized as sets of simple rules. L-systems are sets of rules and symbols that model such growth processes. The name L-system is short for "Lindenmayer's system", after Aristid Lindenmayer, who was one of the first people to use syntactic methods to model growth. Originally they were devised to provide a formal description of the development of simple multi-cellular organisms and to illustrate the neighborhood relationships between plant cells. Later on, this system was extended to describe higher plants and complex branching structures.
L-systems consist of an axiom (a simple string like "f"), and a set of production rules (such as "f=f-f++f-f"), and also an alphabet of symbols which have some pre-defined meaning and interpretation. The axiom is recursively expanded a fixed number of times according to the rules, after which a long string is generated. By increasing the recursion level the form slowly 'grows' and becomes more complex. Note, this is what makes fractal and recursive forms so easy to describe in an L-system.
Example: original Lindenmayer L-system for his algae:
rules: A = AB, B = A
produces the following generations when you start with the string "A":
level 0: A level 1: AB level 2: ABA level 3: ABAAB level 4: ABAABABA
The resulting string by itself is useless unless some meaning or interpretation is made of it's symbols. By giving the symbols A and B different meanings, one can produce different interpretations of the growth. For this application, we will use the programming language LOGO to draw pictures that represent our L-systems. LOGO was invented by Seymour Papert as a system for translating a sequence of symbols into the motions of an automaton robot (the "turtle") on a graphics display; the original idea was to provide a programmable object with which children could learn to think geometrically. This also turns out to be an ideal system for giving a geometrical interpretation to the dynamics of L-systems.
For example, consider the following rules:
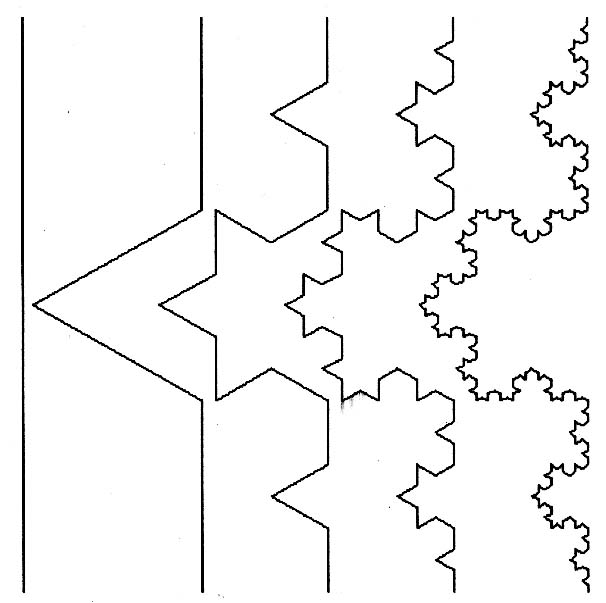
start: f rules: f = f-f++f-f level 0: f level 1: f-f++f-f level 2: f-f++f-f-f-f++f-f++f-f++f-f-f-f++f-f level 3: f-f++f-f-f-f++f-f++f-f++f-f-f-f++f-f-f-f++f-f-f-f++f-f++f-f++f-f-f-f++f-f++f-f++f-f-f-f++f-f++f-f++f-f-f-f++f-f-f-f++f-f-f-f++f-f++f-f++f-f-f-f++f-f
Traditionally, "f" means to go forward (drawing a line from the current point to the next point), while "+" and "-" mean to turn (right or left). As you can see, using an axiom and a few rules, it is possible to construct very complex and interesting fractals. The turtle is usually defined by its position and heading.
For this project, you only need to know a few LOGO commands:
|
Command |
Description |
|---|---|
|
FD dist |
moves the turtle forward by dist pixels |
|
BK dist |
moves the turtle backwards by the amount specified |
|
LT degrees |
turns the turtle counterclockwise by the specified angle |
|
RT degrees |
turns the turtle clockwise by the specified angle |
|
PD |
sets the pen's position to DOWN |
|
PU |
sets the pen's position to UP |
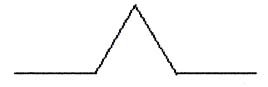
Thus, for level 1 of the example above, your program should generate the following output (assuming "f" means go forward ten steps, "+" means turn right thirty degrees and "-" means turn left thirty degrees):
fd 10 lt 30 fd 10 rt 30 rt 30 fd 10 lt 30 fd 10
which produces the following picture when run through a logo interpreter (such as ~rcduvall/bin/logo or available for download here):

and the progression of generations looks like the following:
It is important to note that LOGO does not require any punctuation other than white space and that every command has an opposite that allows you to "undo it" (fd 10 and bk 10, lt 20 and rt 20, pu and pd). To quit logo, use the command "bye".
The result of evaluating an expression in this application is a string that should be interpreted by LOGO. Thus, it will not be practical to print the string to the console after each command. Instead, you should save the result of the expression in a temporary file and use a program (like logo) to display the results. If the user likes the result, they may want to save it to a real file themselves (via the display program).
Your program should recognize the following expressions:
| expression |
|
semantics |
|
|---|---|---|---|
| Constant |
[0-9]+ |
an integer constant |
87
13 0 |
| String |
between quotes> |
strings are passed directly to the LOGO interpreter |
"fd"
"rt 10 fd 10" |
| Variable |
[a-zA-z_*&^%$+-@!/><]+ |
an expression represented by a word By default the following variables are defined distance // 10 angle // 30 f // "pd fd" distance g // "pu fd" distance + // "rt" angle - // "lt" angle |
f
bugs |
| Assignment |
|
assigns an expression to a variable Note, these assignments should not be circular (i.e., no a = a + 1) |
lt = "lt"
a = bugs |
| Rule |
|
a rule generates a list of variables and strings to be evaluated Note, these assignments will typically be circular (i.e., a = ab) Note, rules can have the same names as variables |
a -> ab
f -> f-f++f-f |
| Binary Function |
|
a function that takes two arguments; the first of
which is an rule and the second is shown below
expand(rule, const) // expand rule given number of times |
expand(f,2)
|
| Stack Operator |
|
do, then undo, the generated LOGO commands within the braces so the turtle's position and heading appears unchanged after the commands have been executed |
F[+G][-G]F[+G][-G]FG |
| New Functions | define functions with the following semantics
random() // create random rule mutate(rule) // create new rule from old by introducing random expressions mate(rule, rule) // create new rule from "parents" by randomly combining |