Ray Tracing Homework
Please submit
your homework electronically using the name hw1. You may
use any medium with which you feel comfortable to complete your work. In
the past, people have written programs, used applications such as Mathematica
or Matlab, or formatters such Microsoft Word or LaTEX. However, you should
submit only code, plain text, HTML, or PDF, and possibly image (gif or jpeg)
files. Your submission must represent your own work and must include
credit for any print or electronic resources used.
Problem 1
Give the t values of the intersections of each of the
following three rays with each of the following two surfaces (for a total of
six intersection calculations). Also compute the actual intersection points
given the computed t values. Note which of the two
surfaces (if any) would be hit first by each ray in a ray tracer?
Ray (origin, direction) |
Surface |
|---|---|
| ((0, 0, 0), (1, 1, 1)) | a sphere of radius 1.25 centered at (1, 1, 1) |
| ((0, 0.001, 0.001), (1, 0, 0)) | a triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1) |
| ((0.001, 0, 0), (0, 1, 1)) |
Problem 2
Assume a sphere of radius 1 is illuminated by a light source 3 units away and viewed by a camera 5 units away (both distances measured from the center of the sphere). The camera, the source, and the center of the sphere lie in a horizontal plane. The angle between the directions to the camera and light source is θ:
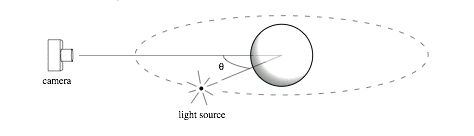
Suppose we render an image using this camera. The sphere will appear as a circle in the image. Consider the color in the image at the center of the rendered sphere and at the right edge of the rendered sphere.
- For what range of values of θ is the Lambertian (diffuse) shading on the sphere non-zero at the right edge? At the center? For what values of theta is it maximized in each of those two places?
- Answer the same questions for the specular component of the Phong (specular) model, with exponent n = 40.
Define θ as the counterclockwise angle from the camera to the light—that is, θ < 0 when the source is on the left of the camera, θ > 0 when then source is on the right of the camera, θ = 0 when the source is right in front of the camera, and θ = ±180? when they are opposite one another. Feel free to round your answers to the nearest degree.

