Homework 2: Transformations
You may use any medium with which you feel comfortable to complete your work. In the past, people have written programs, used applications such as Mathematica or Matlab, or formatters such Microsoft Word or LaTEX. However, you should submit only code, plain text, HTML, or PDF, and possibly image (gif or jpeg) files. Your submission must represent your own work and must include credit for any print or electronic resources used. Please submit your homework electronically.
For problem 1 you should specify the transformations as matrices, but for problems 2 and 3 you should describe them (precisely) in words—for example, “nonuniform scale by 5 in x and 2 in y” or “rotation by 45 degrees about point (1, 2).”
Problems
Suppose you are trying to model a flower from the following nine objects. Each ellipse can be thought of as an instance of the unit circle, transformed by a different 2D affine transformation. The major and minor diameters of the ellipses are all integers. All the parts centered on the y axis have integer or half-integer center points.
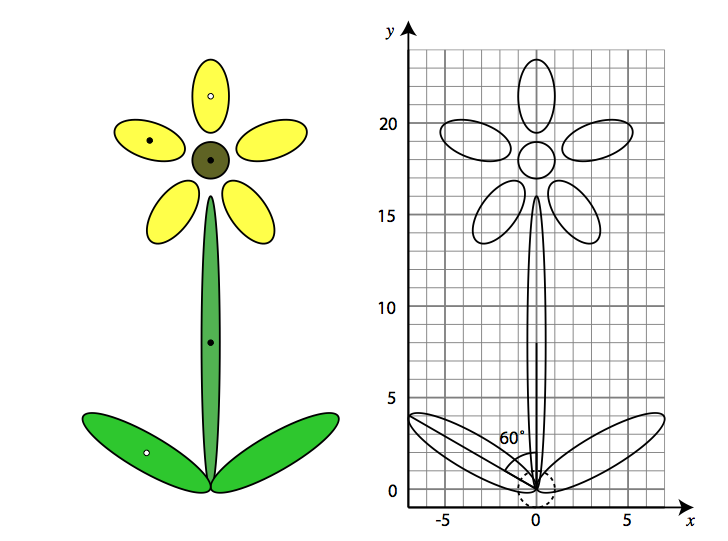
- Derive the 3x3 transformation matrices that place each of the five parts marked with a dot into the world coordinate system shown on the right?
- Express the transformations for only the leaf and petal marked with a white dot as
- a sequence of transformations consisting of translations, rotations about the origin, and nonuniform scales about the canonical axes
- a single nonuniform scale with respect to an arbitrary center and axis
This drawing can also be expressed in a more structured way, as a set of grouped and transformed instances of the unit circle according to the following scene graph.
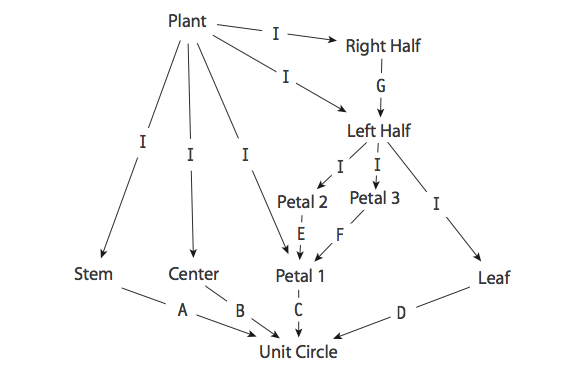
Each edge of this graph has a transformation associated with it.
- If all the transformations labeled I are identity transformations, describe the lettered transformations A, . . . , G.
(You can cross-check against your answer for problem 1 by confirming that multiplying the matrices of the transformations along each of the nine paths from “Plant” to “Unit Circle” leads to the matrices that place the nine parts of the drawing in world coordinates.)

