PLU is LU with pivoting (although ``P'' stands for
permutation).
- Permutation matrices
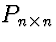 :
:
- Each row or each column has exactly one 1 and for the rest.
- Example:
![$\left[ \begin{array}
{ccc}
0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & 1
\end{array} \right]$](img65.gif)
- Property: PT P = P PT = I
- What if a11 = 0 happens in LU-factorization?
- Want to find a permutation matrix P, such that A = PLU.
- Algorithm
- 1.
- If n = 1, return P = 1, L = 1, U = a11.
- 2.
- Find a non-zero element ai1 in the first row of A.
(If not, then the system is not solvable.)
- 3.
- Define a permutation matrix
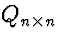 such that
such that
- q1i = qi1 = 1,
- qjj = 1 for
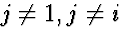 ,
, - All the other elements of Q are 0.
- 4.
- Let B = QA. Notice that
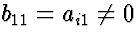 .
. - 5.
- Write B as
![\begin{eqnarraystar}
B & = & \left[
\begin{array}
{cc}
b_{11} & r^T \ c & B'
\end{array} \right].
\end{eqnarraystar}](img69.gif)
- 6.
- Define
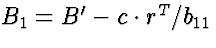 . Recursively compute B1 = P1 L1 U1
. Recursively compute B1 = P1 L1 U1
- 7.
- Return
![\begin{eqnarraystar}
P \; = \; Q^T \left[
\begin{array}
{cc}
1 & 0 \ 0 & P_1...
...n{array}
{cc}
b_{11} & r^T \ 0 & U_1
\end{array} \right]
\end{eqnarraystar}](img71.gif)
- Correctness of the algorithm? By induction.
- Operation count? Same as LU.



Next: Summary
Up: SOLVING LINEAR SYSTEMS
Previous: LU-factorization
![$\left[ \begin{array}
{ccc}
0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & 1
\end{array} \right]$](img65.gif)
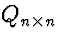 such that
such that
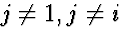 ,
,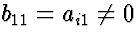 .
. ![\begin{eqnarraystar}
B & = & \left[
\begin{array}
{cc}
b_{11} & r^T \ c & B'
\end{array} \right].
\end{eqnarraystar}](img69.gif)
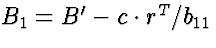 . Recursively compute B1 = P1 L1 U1
. Recursively compute B1 = P1 L1 U1
![\begin{eqnarraystar}
P \; = \; Q^T \left[
\begin{array}
{cc}
1 & 0 \ 0 & P_1...
...n{array}
{cc}
b_{11} & r^T \ 0 & U_1
\end{array} \right]
\end{eqnarraystar}](img71.gif)