CompSci 100e Spring11
Classwork 13: How Many BSTs?

Name & NetID: ___________________________________

Name & NetID: ___________________________________

Name & NetID: ___________________________________

1. In a complete binary tree, every non-leaf node has two children, and all the leaves are at the same level. Two examples of complete trees are shown below.

   

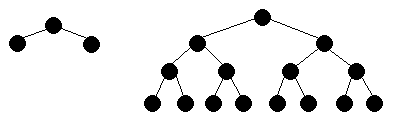
   If there are n levels in a complete tree (the tree on the left above has two levels, the tree on the right has four) what is the total number of nodes in the complete tree (both leaves and internal nodes) and the total number of leaves in the complete tree. Express answers in terms of n.

2. The pre-order traversal of a binary tree (not a search tree) is as follows:

      x p q r s a d k z o
   

   The in-order traversal of the same tree is the following, draw the unique binary tree with these pre- and in-order traversals.

     q p r s x d k z a o
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

3. There is one binary tree with one node. There are two differently shaped trees with two nodes. There are 14 different (shaped) binary trees with four nodes. These different trees are shown below.

   

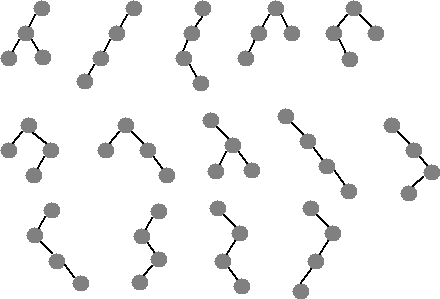
   1. Draw all five of the different binary trees with three nodes.

   2. Using the information about how many trees there are with 1, 2, 3, and 4 nodes determine how many different binary trees there are with 5 nodes. Do not draw them, but reason about how many there must be based on:
      • There is a root node.
      • There are four other nodes that are distributed between the left and right subtrees.
      For example, there must be 28 different five-node trees in which all the nodes but the root are either in the left subtree or all in the right subtree (why?)

   3. Can you make a different number of legal BSTs with different elements? That is, can you make a different number of trees with the elements (1,1,1) vs. (1,2,3) vs. (-4,72,0)? Why or why not?

   4. Complete the BST count APT. Will you solution return an answer in under 3 seconds for trees with 25 elements?