In the first lecture about Java programming we had used the factorial mathematical function for one of my demo programs. Recall that the value 7! (seven factorial) is calculated as 7! = 7*6*5*4*3*2*1 = 5040. How can I rigorously define the factorial function? I could say that n! = "n multiplied by each of the numbers from 1 to n-1". This gets the idea across, but there's also another clear mathematical way I can define it.
n > 0:
n! = n*(n-1)!
This definition that I've just given for factorial is a recursive definition. It uses the factorial function within the definition for the factorial function. Does this actually work? Certainly. When given a value for n I can just insert that value into the definition above and calculate the value of n!. Using n = 7, we just have that 7! = 7*6!. What's 6! equal to? 6! = 6*5!. ...and so on until we get to 1! = 1. Then, once we're down to 1!, we can build back up:
Rolling out the definition:
7! = 7 * 6!
7! = 7 * (6 * 5!)
7! = 7 * (6 * (5 * 4!))
7! = 7 * (6 * (5 * (4 * 3!)))
7! = 7 * (6 * (5 * (4 * (3 * 2!))))
7! = 7 * (6 * (5 * (4 * (3 * (2 * 1!)))))
7! = 7 * (6 * (5 * (4 * (3 * (2 * (1))))))
Building our solution:
7! = 7 * (6 * (5 * (4 * (3 * ( 2 * (1) )))))
7! = 7 * (6 * (5 * (4 * ( 3 * (2) ))))
7! = 7 * (6 * (5 * ( 4 * (6) )))
7! = 7 * (6 * ( 5 * (24) ))
7! = 7 * ( 6 * (120) )
7! = 7 * (720)
7! = 5040
There are two parts to the recursive definition I gave above: a recursive step and a base case. The recursive step was defining n! = n*(n-1)!. This is the part of the definition that I use for most of the steps of calculating n-1!. The base case was defining 1! = 1. It was only used once, but having that base case is very important. Without it our recursion would never end and we would have infinite recursion.
Infinite recursion occurs when we've got a recursive statement that will keep referring to itself forever. How does recursion avoid that anyway? Recursion works because the recursive statement keeps referring to smaller and smaller instances of itself. Eventually, the instance gets so small that we reach a base case and can stop.
In the case of calculating n!, the recursive step referred to (n-1)!. This is guaranteed to be a smaller instance of the factorial function since we only dealt with positive integers. This also allowed us to eventually reach a base case: 1! = 1. The recursive step must recurse on smaller instances of itself so that it can progress towards a base case. If we never hit a base case then the recursion never stops and we get infinite recursion.
Recursion may seem like it does the same work as an iterative solution. Before we used an iterative solution (a for-loop) to compute factorials in a program. Can recursive solutions solve problems that iterative solutions can't? Not really. Can some problems be solved much more easily with recursion than with iteration? Definitely. Computing factorials wasn't one such case, but we'll see some later in the lecture.
Previously, to solve factorials we used the Math4.java program. It used a for-loop to solve the problem iteratively. Now we're going to use another program, RecFact.java, to solve the problem recursively.
RectFact.java operates just like Math4.java, but now the for-loop has been replaced by a call to the factorial method. For this method, if the input value is 1, it simply returns 1. Otherwise it multiplies the input value against the value returned by the method call factorial(n-1). Note how this mirrors our recursive definition for factorials.
For integer values of n > 0:
long m;
if(1 == n)
return 1;
else {
m = factorial(n-1);
return n * m;
}
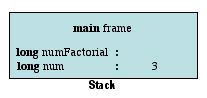
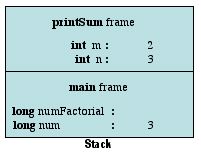
One important thing to note is how these calls are actually played out when the computer runs our code. Remember how every method call gets its own stack frame? Calls to a recursive method are no different. Each new call to the method is unique, so each gets its own unique stack frame. For an example, here's a run of RecFact.java with a user input of 3. The addition of the middle-man variable m will help to show how things are woking in our stack frame. First up, the main method's stack frame. This is right before the call to the factorial method.

Now, we get our first call to the recursive method, this time with an input value of 3. A frame for that call to factorial is now pushed onto the stack.
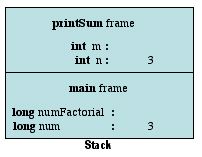
Since we have no clue what random 0's and 1's the variable m might be holding I've given it a blank value for now. The method's behavior is more important at this point. It checks and finds the the value of n is not equal to 1. Thus, it recursively calls factorial(2). This then adds a new stack frame to our picture.
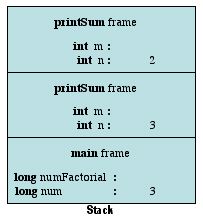
We've now got 2 different stack frames for two different calls to the factorial method. Each frame has separate versions of the n and m variables. The only thing that is the same is the method's code (and in this case, it's behavior). Again, the value of n is not equal to 1, so the method recursively calls factorial on the value of n-1. This gets us one last stack frame.

For this last call to factorial the value passed into the variable n is 1. This hits our base case and the method simply returns the value of 1. Now we start popping off the stack frames and storing values in the m variables.
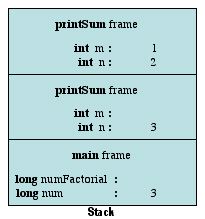
The variable m in the topmost stack frame now holds the value 1. This was returned from the stack frame we just popped off. The call to the factorial method represented by the topmost stack frame now multiplies the values of n and m together and returns the result. This allows us to pop off this stack frame and store the returned value in the stack frame below.
factorial method call. It multiplies m by n and returns its value. It's stack frame is then popped off and the returned value, 6, is stored into the numFactorial variable in the main method's stack frame.
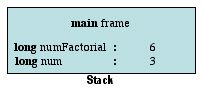
The main method is now free to print out the value it has obtained. That will be the last line of code, cause this last stack frame to be popped off, and the program will end.
We've now talked about recursion, seen a recursive program, and seen the stack frames of that recursive program in action. One more thing: is recursion ever that useful? Finally, here's a case where it is: the Towers of Hanoi problem.
In the Towers of Hanoi problem we've got 3 towers and some number n of disks starting on the first tower. The disks are all different sizes and are stacked in decreasing order of size (largest at the bottom). The goal is to move all of the disks from the first tower to the second tower. There's a catch: we can only move one disk at a time AND we can't stack a larger disk on top of a smaller one.
How do we solve this problem iteratively? It's very difficult to design such a program. However, this is much easier to solve with recursion. Luckily, that's the solution method you'll be working on for today's lab.