Given a source node s and a destination t, we want to find the shortest (minimum weight) path from s to t.
En route, we will find the shortest path to all nodes ![]() .
.
Solution is a sequence of nodes ![]() such that v1 =
s, vl = t, and
such that v1 =
s, vl = t, and 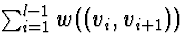 is minimized.
is minimized.
Definition: ![]() is the length of the shortest path from
u to v. So, we're looking for a path from s to t whose length
is
is the length of the shortest path from
u to v. So, we're looking for a path from s to t whose length
is ![]() .
.
Example graph...