Variations

Some simple variations:

• How find any path from s to t?

• How find shortest path if w(u) = 1 for all $u\in V$?

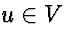• How find shortest path if G is acyclic?

More complex variations that we'd look at if we had time:

• All-pairs shortest path: How can you compute shortest paths for all pairs s, t in less time than it takes for |V| single-source shortest-path runs?
• Stochastic shortest path: What if there is a probability that you'll leave u headed for v but end up at r instead?
• Negative edge weights: What if traversing some edges actually improves your driving time?