When you submit your work, follow the instructions on the submission workflow page scrupulously for full credit.
Instead of handing out sample exams in preparation for the midterm and final, homework assignments include several problems that are marked Exam Style . These are problems whose format and contents are similar to those in the exams, and are graded like the other problems. Please use these problems as examples of what may come up in an exam.
As a further exercise in preparation for exams, you may want to think of other plausible problems with a similar style. If you collect these problems in a separate notebook as the course progresses, you will have a useful sample you can use to rehearse for the exams.
Is this assignment properly formatted in the PDF submission, and did you tell Gradescope accurately where each answer is?
This question requires no explicit answer from you, and no space is provided for an answer in the template file.
However, the rubric entry for this problem in Gradescope will be used to decuct points for poor formatting of the assignment (PDF is not readable, code or text is clipped, math is not typeset, ...) and for incorrect indications in Gradescope for the location of each answer.
Sorry we have to do this, but poor formatting and bad answer links in Gradescope make our grading much harder.
Various measures of impurity have been proposed for decision trees in the literature, both for classification and for regression. Differences between them are often subtle, and there are no clear criteria for which measure to use for a particular problem. Of course, the questions can always be settled empirically by cross-validation.
In principle, measures of impurity that are defined for classification can be used for regression as well, and vice-versa, as explained next.
Given a set of training samples, impurity quantifies the diversity of labels for classification and of values for regression. The distribution of labels is a discrete distribution $p(y)$ for $y\in Y$, where $Y$ is a categorical set. The distribution of values in a regression problem is generally a continuous distribution over $\mathbb{R}$. However, this distribution can be quantized into a histogram by subdividing $\mathbb{R}$ (or at least the part of it that is relevant to the problem) into disjoint bins. The histogram is then also a discrete distribution, so whatever we say about label impurity we can also say for (approximate) value impurity.
Here are a few definitions of impurity measures for a set $S$ of labels or values, based on a discrete distribution $p_k$ where the vector of labels or value bins has $K$ elements $k = 0, \ldots, K-1$
Error rate: $i_r(S) = 1 - \max_{k=0, \ldots, K-1} p_k$.
Gini index: $i_g(S) = 1 - \sum_{k=0}^{K-1} p_k^2$.
Entropy: $i_e(S) = - \sum_{k=0}^{K-1} p_k \log_2 p_k$.
Variance: $i_v(S) = \sum_{k=0}^{K-1} (k - m)^2 p_k$ where $m = \sum_{k=0}^{K-1} k p_k$ is the mean.
While $\log_2 p_k$ is undefined when $p_k = 0$, it is easy to see that $\lim_{p\rightarrow 0} p \log p = 0$, so we define $p_k\log_2 p_k = 0$ when $p_k = 0$ in the expression for entropy.
One way to visually compare different impurity measures is to see what they do in the simplest possible case, in which the set of labels or value bins has two elements, $K = 2$. Then, the distribution has two values $p_0$ and $p_1$ where $p_0 + p_1 = 1$. To simplify notation in this problem we redefine $q = p_0$ and $p = p_1$, so that $p + q = 1$ (note that $q$ comes first). Also, let $Y = \{0, 1\}$.
Write code to plot the four impurity measures above as a function of $p$ for the case $K=2$.
Your plots should be on a single diagram. Label the horizontal axis and add a legend that specifies which plot is for which measure. Give title 'impurities' to the plot.
You may want to define a function that plots four given impurities given a list of them with their names, plus a plot title. This is because you will be asked to plot variations of the four impurity measures above. This code structure is not required, though.
Clearly what matters in a definition of impurity is the ratio between any two values of it, rather than the individual values by themselves. That is, any impurity measure is equivalent to the same measure scaled by a positive constant.
To compare the four impurities above more meaningfully, make a plot that instead of showing impurities $i(S)$ as you did in the previous problem shows $\hat{i}(S) = i(S) / \max_{p\in[0, 1]}i(S)$. That is, the new plots are normalized by the largest value that they achieve as $p$ varies between $0$ and $1$.
Your plot should be in the same style as in the previous problem. Give title 'scaled impurities' to the plot.
If you did things correctly, then two of the scaled plots in the previous problem are identical to each other, and one of them is not visible because it is hidden behind the other. State which of the two plots are identical and then prove mathematically (for the case $K = 2$) that they are.
The first three impurity measures given in the preamble to this part require storing the distribution $p_0,\ldots, p_{K-1}$. The variance $i_v(S)$, on the other hand, can be computed directly from the values $y_0, \ldots, y_{N-1}$ in the set $S$, which is assumed to contain $N$ samples.
Give an alternative formula for $i_v(S)$ in terms of $y_0, \ldots, y_{N-1}$. This formula has one expression for the mean $m$ and second expression for $i_v(S)$ that contains $m$.
Then write code that prints out the values obtained with the two formulas for $i_v(S)$ for the labels in the vector S defined below (for $K=3$ and $Y = \{0, 1, 2\}$. Of course, the two values are expected to be the same.
import numpy as np
K = 3
Y = np.arange(K)
S = [0, 1, 1, 0, 0, 1, 0, 0, 2, 1, 1, 0, 2, 1, 0, 0]
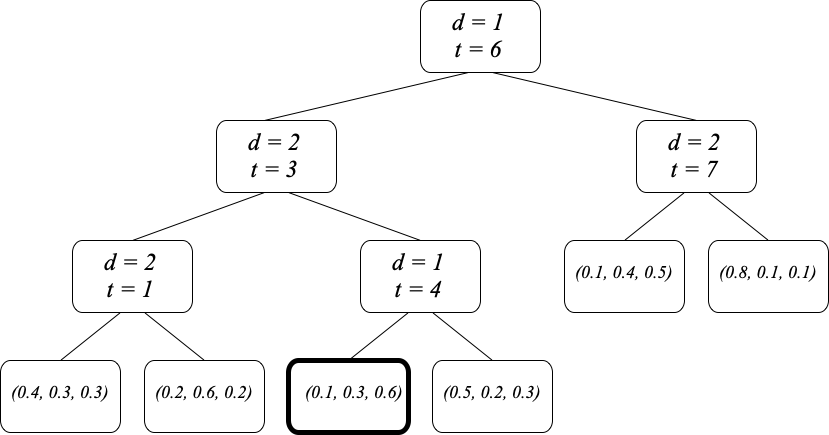
numpy function that simplifies your code.The decision tree in the Figure below is used to classify points $\mathbf{x}$ in $X=\mathbb{R}^2$ into one of three categories in the label set $Y = \{1, 2, 3\}$. The internal nodes of the tree store the split dimension $d\in\{1, 2\}$ and split threshold $t\in\mathbb{R}$. Elements at or below threshold go to the left sub-tree. Each leaf stores a normalized histogram $\mathbf{p} = (p_1, p_2, p_3)$ of the labels in the training set $T$ that fall into that leaf. The decision tree implements the classifier $h(\mathbf{x})$.

Give the numerical value of $h((5, 2))$ i.e., $\mathbf{x} = (5, 2)$, find $h(\mathbf{x})$
Give a numerical estimate of the probability that the value of $h((5, 2))$ found above is wrong, based on the values given in the tree.
Give the exact numerical values of the error-rate impurity $i_e(S)$ and of the Gini index $i_G(S)$ at the leaf with a thick boundary in the Figure above.
The following small set $S$ of four samples has data points in $\mathbb{R}^2$ and labels in $Y = \{1, 2, 3\}$: $$ S = \{(\mathbf{a}, 1), (\mathbf{b}, 2), (\mathbf{c}, 2), (\mathbf{d}, 3) \} $$ as shown in the figure below.
The coordinates of these points are shown along the axes and the labels are indicated next to their names.
For instance, point $\mathbf{b}$ has coordinates $(x_1, x_2) = (4, 6)$ and label 2.
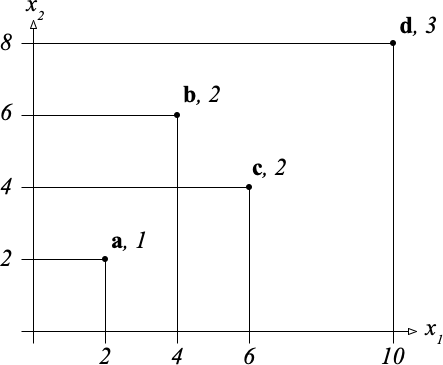
A split of the diagram above is either a vertical or a horizontal line that splits the set of four points into two subsets in a nontrivial way (that is, both subsets are nonempty).
The split is a maximum-margin split if it is equidistant from the two nearest points in $S$.
First give the numerical value of the impurity $i(S)$ of the entire set $S$, using the error rate as the measure of impurity.
Then complete the table below. The table lists all the possible maximum-margin splits for this training set, starting with all the vertical lines. For each splitting direction, the lines are listed in order of increasing coordinate $x_j$, one line per row of the table.
Each row of the table contains the following information:
The impurity decrease $\delta$ is defined in equation (2) of the class notes on trees and forests. "Left" and "right" are also defined in those notes.
If there are multiple splits with best decrease in impurity, say yes to all of them in the "best" column.
The first row is partially filled out for you (you do the last column). Use fractions of integers to express rational numbers.
The files tree.py and draw.py retrieved below contain respectively a rudimentary implementation of a decision tree and some utility functions that are useful for drawing data samples or trees when the data points live in $\mathbb{R}^2$. The file classification_data.pickle, which is loaded into the dictionary classification_data below contains a training set and a test set with data points in $\mathbb{R}^2$.
from urllib.request import urlretrieve
from os import path as osp
def retrieve(file_name, semester='fall22', course='371', homework=9):
if osp.exists(file_name):
print('Using previously downloaded file {}'.format(file_name))
else:
fmt = 'https://www2.cs.duke.edu/courses/{}/compsci{}/homework/{}/{}'
url = fmt.format(semester, course, homework, file_name)
urlretrieve(url, file_name)
print('Downloaded file {}'.format(file_name))
import pickle
classification_file = 'classification_data.pickle'
for file_name in ('tree.py', 'draw.py', classification_file):
retrieve(file_name)
with open(classification_file, 'rb') as file:
classification_data = pickle.load(file)
Using previously downloaded file tree.py Using previously downloaded file draw.py Using previously downloaded file classification_data.pickle
The dictionary classification_data has the usual format: A training set classification_data['train'] and a test set classification_data['test'], each with keys x and y for data points and labels.
Differently from previous assignments, this dictionary also has keys 'y range' and 'type'. The value corresponding to key 'type' is a string that is set to 'classification' for this and any other classification data set. For a regression problem this string is set to 'regression'.
The numpy vector corresponding to key 'y range' gives the minimum and maximum value for the labels or values in the data set. For a classification problem, the two entries of this vector are 0 and $K-1$ where $K$ is the number of labels. For a regression problem, these two entries are two real numbers between which every value is expected to be. This vector is used by draw.colormap to construct a color map suitable for displaying points in the data set and predictor decision regions.
Here is how some of the code in draw.py can be used to display the training set in classification_data:
from draw import colormap, sample_plot
from matplotlib import pyplot as plt
%matplotlib inline
def draw_samples(samples, y_range, title=None):
cmap = colormap(y_range)
plt.figure(figsize=(7, 7), tight_layout=True)
sample_plot(samples, cmap, 12)
plt.axis('off')
plt.axis('equal')
if title is not None:
plt.title(title, fontsize=16)
training_set = classification_data['train']
y_range = classification_data['y range']
data_type = classification_data['type']
draw_samples(training_set, y_range,
'{} training samples'.format(data_type))
The code in tree.py retrieved above implements decision trees by following quite closely the recursive version described in the class notes.
The main difference is that the top-level functions tree_train (called treeTrain in Algorithm 2 in the notes) and predict (in Algorithm 1) also expect a parameter config. This is a dictionary that specifies the constants $s_{\min}$ and $d_{\max}$ in find_split (called findSplit in Algorithm 2) as well as two functions distribution and impurity.
The function distribution returns the distribution of sample labels or values in some set, and impurity is the impurity measure to use during training.
In addition, for classification problems, the entry config['K'] is also defiined and is set to the number of labels.
Here is an example of how such a configuration dictionary can be defined:
import numpy as np
def categorical(samples, config):
p = [np.count_nonzero(samples['y'] == c)
for c in range(config['K'])]
return np.array(p, dtype=float) / np.sum(p)
def error_rate(samples, config):
return 1. - np.amax(categorical(samples, config))
training_config = {
'min samples': 1,
'max depth': np.inf,
'distribution': categorical,
'impurity': error_rate,
'K': y_range[1] - y_range[0] + 1
}
We can now train the tree as a classifier with the given configuration parameters:
from tree import train_tree
t = train_tree(training_set, 0, training_config)
Since training_config specifies 1 as the minimum number of samples in a leaf and sets the maximum tree depth to infinity, this tree fits the training data with zero risk, but does somewhat worse on the test data.
To check this, we need to specify a summary function and a loss to be used for performance evaluation.
As usual for a classifier, we use the majority function as a summmary function and the zero-one loss:
def majority(p):
return np.argmax(p)
def zero_one_loss(y, y_hat):
return float(y != y_hat)
from tree import predict
def performance(t, summary, samples, loss):
xs, ys = samples['x'], samples['y']
ys_hat = [predict(x, t, summary) for x in xs]
losses = [loss(y, y_hat) for y, y_hat in zip (ys, ys_hat)]
risk = np.mean(losses)
return risk
for which, samples in (
('training', classification_data['train']),
('test', classification_data['test'])
):
risk = performance(t, majority, samples, zero_one_loss)
print('{} {} risk {:.3f}'.format(data_type, which, risk))
classification training risk 0.000 classification test risk 0.012
As a warmup problem, write a recursive function with header
def count_leaves(tau):
that takes a decision tree tau and returns the number of its leaf nodes. Show your code and print out what it returns for the tree t trained above.
is_leaf from tree. This is the same as leaf? in Algorithm 1 in the notes.tau is an internal node, its children are tau.left and tau.right, corresponding to $\tau.L$ and $\tau.R$ in the class notes.The function paint_tree defined below is a partial implementation of a procedure that uses sample_plot (imported earlier) to draw a set of samples specified in samples (either a training set or a test set in the format above) and then colors the decision regions of the given tree tau.
The function includes the line
# paint_subtree(tau, box, summary)
This line is commented out because implementing paint_subtree is your job.
Show your implementation of paint_subtree and the result of the calls
title = 'Partition of {} training set'.format(data_type)
paint_tree(t, training_set, majority, y_range=y_range, title=title)
(of course after uncommenting the paint_subtree line in paint_tree).
from draw import Box
def paint_tree(tau, samples, summary, y_range, title=None):
assert tau.j < 2, 'Can only draw two-dimensional trees'
cmap = colormap(y_range)
plt.figure(figsize=(8, 8), tight_layout=True)
box = Box(samples['x'], cmap=cmap)
plt.plot((box.left, box.right, box.right, box.left, box.left),
(box.down, box.down, box.up, box.up, box.down), 'k',
linewidth=0.5)
# paint_subtree(tau, box, summary)
sample_plot(samples, cmap, 5)
plt.axis('off')
plt.axis('equal')
if title is not None:
title += ' ({} boxes)'.format(count_leaves(tau))
plt.title(title, fontsize=16)
plt.show()
paint_subtree recursively: If you are at a leaf, paint its box (see box.paint below). Otherwise, use the splitting dimension tau.j and the splitting threshold tau.t in the current internal node tau to detemine the boxes for the left and right child (see Box class below). Then recurse down the two subtrees. draw.py retrieved earlier implements a Box class that represents a rectangle in data space through attributes left (minimum $x$), right (maximum $x$), down (minimum $y$) and up (maximum $y$). The function paint_tree above initializes Box with a bounding box around the data points given in samples and a suitable colormap.All you need to know about the Box class is that it also implements attribute functions but_with and paint.
box.but_with takes the four bounds for box and returns a brand-new box where one or more of the bounds is replaced by a new value. For instance, if box has left = 1, right = 5, down = 2, up = 7, then box.but_with(right=4) is a new box with bounds left = 1, right = 4, down = 2, up = 7 and the same colormap as box.box.paint(value) draws the box in a color that corresponds to the given value. If the node tau in a tree is a leaf node, then istead of children tau.left and tau.right it contains a distribution tau.p (a value like that returned by the function specified by your 'distribution' configuration parameter). So you would retrieve value as follows:
value = summary(tau.p)Train a new tree with training_config['max depth'] equal to 3. Everything else remains the same, including the training and test data. Show training and test risk and paint the new tree.
Let us use the same code as above for a regression problem. Here is some data:
regression_file = 'regression_data.pickle'
retrieve(regression_file)
with open(regression_file, 'rb') as file:
regression_data = pickle.load(file)
Using previously downloaded file regression_data.pickle
training_set = regression_data['train']
y_range = regression_data['y range']
data_type = regression_data['type']
draw_samples(training_set, y_range,
'{} training samples'.format(data_type))
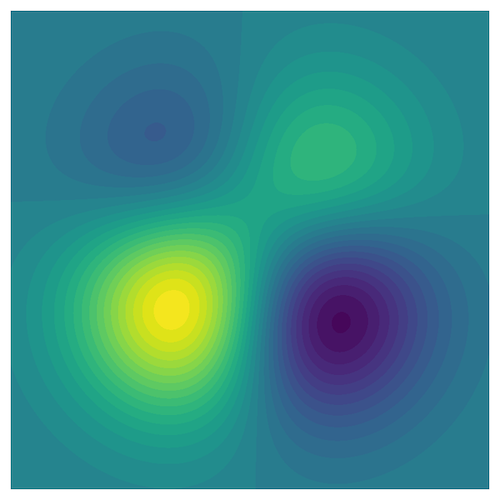
Just so you know, here is a color coding of the function from which the data is drawn (at random). The domain is the unit square.
Define functions with the following headers:
def normal(samples, _):
def variance(samples, _):
def mean(p):
def quadratic_loss(y, y_hat):
and the following specifications:
normal will be the distribution in training_config. It takes a data set samples (either training or test) and returns a dictionary that represents its distribution in the form of a dictionary. The dictionary has keys 'mean' and 'variance' and the corresponding values are the sample mean and variance of the values in samples['y']. The function normal ignores its second argument.variance will be the impurity in training_config. It takes a data set samples (either training or test) and returns the sample variance of the values in samples['y']. The function variance ignores its second argument.mean will be the summary function used by predict. It takes a distribution (as returned by normal) and returns its mean (so mean just looks up a dictionary). Note that mean does not take a set of samples as input.quadratic_loss will be the loss function used by performance. It takes a true value y and a predicted value y_hat (both real numbers) and returns the quadratic loss.Train the decision tree with the configuration parametrs specified above and with $s_\min = 1$ and $d_\max = \infty$ on regression_data, evaluate and print out its training and test performance, and paint the tree.
The tree will be painted in fainter colors than those shown in the figure above, to ensure that the data points superimposed onto the paint are still visible.
Let us explore random decision forests through a classification problem that is harder than the one in classification_data, but still with data points in $\mathbb{R}^2$ so we can plot things. The labels now are the four colors red, green, blue, and cyan, which are encoded numerically as 0, 1, 2, 3 in spiral['train']['y'] and spiral['test']['y']. The corresponding matplotlib colors r, g, b, c are in spiral['labels'].
spiral_file = 'spiral.pickle'
retrieve(spiral_file)
with open(spiral_file, 'rb') as file:
spiral = pickle.load(file)
Using previously downloaded file spiral.pickle
from draw import draw_spiral
draw_spiral(spiral)
It would be hard to use paint_tree to draw decision regions for random forests, since it is not clear how one would combine the regions from the predictors in the forest. Instead, we now draw approximate decision regions for random forests using the technique that was used in Figure 2, page 5, of the class notes on nearest-neighbor predictors.
You can do that with the function coarse_regions imported below.
from draw import coarse_regions
This technique requires predicting the labels for a fine grid of points on the plane. This would be too slow with decision forests that use our rudimentary implementation of decision trees. Instead, we rely on sklearn.ensemble.RandomForestClassifier, which is much more efficient.
Given a predictor h that instantiates this class, we would paint its decision regions as follows:
coarse_regions(h, spiral['labels'])Train (use h.fit) a sklearn.ensemble.RandomForestClassifier on spirals['train'] twice, once with 5 trees and once with 500.
Show your code and make two side-to-side plots in a subplot(1, 2, k) with the decision regions plotted by coarse_regions.
Also print out the test accuracy (use h.predict and sklearn.metrics.accuracy_score) computed on spirals['test'] and the out-of-bag accuracy as a percentage (use h.oob_score_ times 100) for each forest. State which values are for which number of trees.
Use the following parameters in sklearn.ensemble.RandomForestClassifier:
n_estimators=n_estimators
max_depth=None
min_samples_split=2
random_state=0
oob_score=True
where n_estimators is either 5 or 500.
When there are too few trees, the training code may warn that it cannot compute a reliable OOB score. You may either ignore those warnings or suppress them with warnings.catch_warnings() and warnings.simplefilter('ignore'). The warnings, however, will help you for the next problem.
Comment on your results for the previous problem. In particular: