Fibonacci Meets Euclid

What happens when we apply Euclid's algorithm to a consecutive pair of Fibonacci numbers, F(k+2) and F(k+1)?

• Well, if k=1, then the algorithm returns the answer 1 after one recursive call.
• Otherwise, we recurse on F(k+1) and 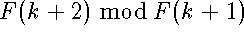. We know that F(k+1) > 1/2 F(k+2), so 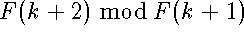= F(k+2)-F(k+1) = F(k). So the next pair Euclid examines is the Fibonacci numbers F(k+1) and F(k).

Example: EUCLID(144,89) = EUCLID(89,55).

How many recursive calls? Exactly k!

Thus, the worst-case time to compute EUCLID(a,b) can be at least 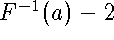(lower bound on worst case).