Fibonacci Upper Bound

But the Fibonacci sequence also gives us an upper bound on the worst case.

Theorem: If EUCLID(a,b) takes recursive calls, then and .

• k=1: To have at least one recursive call, we must have and .
• : Inductive hypothesis implies EUCLID takes k-1 recursive calls and and .

  

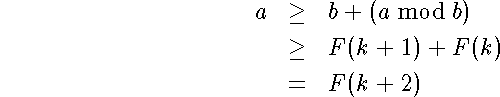
  The first step follows from the fact that is what's left over after removing one or more copies of b from a. So one copy of b plus can't be any bigger than a.

Therefore, we can't take any more than k recursive calls to compute the GCD unless a is bigger than F(k+2). That means that is also an upper bound on the number of iterations needed.