Heaps and Priority Queues
March 6, 2013
Heap Questions
A binary heap is a method of storing a binary tree in an array when the binary tree maintains two properties:
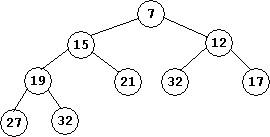
The tree shown below on the left has both the heap shape and the heap property.
Binary trees that are heaps are typically stored in an array. The root of the tree has index one (the array element with index zero isn't used). The children of the root are at indexes two (left child) and three (right child). In general, the children of the tree node with index k have indexes 2k (left child) and 2k+1 (right child).
The binary tree on the left below is stored in a vector as shown on the right.
| Min-Heap | Heap as an array |
|---|---|
|
|

|
Questions
Complete the following questions about heaps using the online form:- Where is the smallest element in a heap (and why?)
- Where is the largest element in a heap (and why?)
- Where is the parent of the element with index 11 when a heap is stored in an array ?
- Where is the parent of the element with index k when a heap is stored in an array?
- If the value 19 in the heap above is changed to 25, is the heap property maintained?
- If the value 21 in the heap above is changed to 13, is the heap property maintained?
- If a new node with 19 is added as the left child of 17 in the heap above, is the heap shape maintained?
Adding an element to a Heap
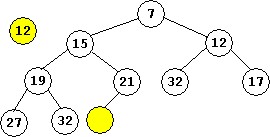
When a new element is added to a heap, both the heap shape and the heap property must be maintained. To maintain the shape, the new element must be added as the last element of the array. This may violate the heap property, so all nodes on the path from the root to the newly added leaf must be checked to see where the new value really belongs, starting from the leaf.This process is shown below for adding the value 12 to the heap.
First, the 12 is shown on the left added to maintain the heap shape. However, the 12 doesn't belong there (the heap property is violated) so the yellow node is shown on the right with no value, the newly added value 12 is "waiting" to find its place as all nodes on the path from the newly added leaf to the root are examined to find where the 12 belongs.

|
|
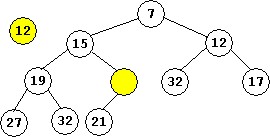
The 12 can't stay as a leaf, so the value in the node above it is moved down to the leaf, and the yellow node conceptually moves up -- this is a new tentative spot for the 12.
|
|
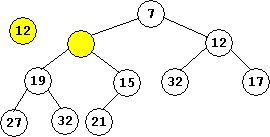
The 12 cannot stay in the location shown above on the left since it is less than 15. The 15 is moved down to the yellow node, and the yellow node conceptually moves up -- this is the tentative spot for the 12 as shown above on the right.
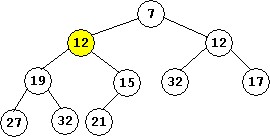
The 12 belongs as the child of 7 (the root) since it is less than the root. The final tree is shown below. The newly-added 12 has been moved up from its original tentative location as a leaf (where the 21 is below) to its final location.
Questions
Complete the following questions about heaps using the online form:
- Suppose new values are added to the last heap above (with 10 elements, the root is 7 that has both children with the value 12).
- If a new value of 20 is added what value is the parent of the 20 node?
- If after adding 20 the value 10 is added what are the values that are children of the root?
- What new values would end up at the root?
- Draw the heap (as an array) that results from adding 12, 7, 11, 9, 15, 10, 8 in that order to an initially empty heap. It may help to draw the heap first.
- Where is the largest element in a min-heap? What is the big-Oh complexity of finding the largest element in the heap? Justify your answer.
Priority Queues
Snarf the code for todays class. You will find the code, RunningJobs.java. Say you have a whole bunch of little jobs that you need to get done. You wrote them all down and you know how long each will take. You want to be able to get the most number of little jobs done as possible, however some are more important to get done than others. This is when a priority queue is great. Complete the code RunningJobs that puts a collection of jobs into a priority queue with their time to complete and priority. Compute the maximum number of jobs you can get done assuming that you need to complete the high priority jobs first. Hints: Complete your compareTo and use a priority queue. There is a toString method in Jobs that may be helpful for debugging. Submit your code for compareTo and numJobsComplete using the following form:The Form.