Recitation 7: Trees
March 1, 2013
Snarf the code for today's recitation and add the following recursive methods to BST.java. There are function calls in main that will help you debug your code, and it may also help to draw the BST that is created in your main method. Complete as many methods as you can before the end of class and submit your code to the Recitation7 submit folder.numLeaves
Write a methodnumLeaves that returns the number of leaves in a binary tree.
public int numLeaves() {
return numLeaves(root);
}
private int numLeaves(IntTreeNode current) {
}
levelCount
Write the method levelCount whose header is provided below. Method levelCount returns the number of nodes on the specified level.
For this problem, the root is at level zero, the root's children are
at level one, and for any node N its level is one more than N's
parent's level.
Hint: when the level is 0, there is always just one node at that level,
the root node (assuming t isn't empty), so return 1. If the level isn't
zero, recursive calls will be used to determine the number of nodes at
the requested level, and the level-requested should change in the
recursive calls.
public int levelCount(int target) {
return levelCount(root, target);
}
/**
* Returns number of nodes at specified level in t, where level >= 0.
* @param level specifies the level, >= 0
* @param t is the tree whose level-count is determined
* @return number of nodes at given level in t
*/
public int levelCount(StringTreeNode t, int level){
}
hasPathSum
Write the methodhasPathSum whose header is given below. Method hasPathSum returns true if there exists some root-to-leaf path in the tree whose root is t whose
nodes sum to target and returns false otherwise.
For example, in the tree shown below there are exactly four root-to-leaf paths. The sums of the paths are 27, 22, 26, and 18. Thus the value of hasPathSum(t,27)
should be true and the value of hasPathSum(t,30) should be false (assuming t points to the root of the tree --- the node whose info field has value 5.)
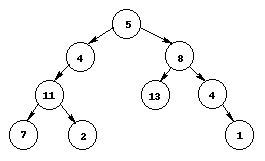
No this is not a binary search tree, but it is a binary tree.
public boolean hasPathSum(int target) {
return hasPathSum(root, target);
}
/**
* Return true if and only if t has a root-to-leaf path that sums to target.
* @param t is a binary tree
* @param target is the value whose sum is searched for on some root-to-leaf path
* @return true if and only if t has a root-to-leaf path summing to target
*/
private boolean hasPathSum(TreeNode current, int target) {
}
findK
Write a method to return the value in the kth element in the tree, assuming elements are ordered following an in-order traversal. From the tree above, an in-order traversal orders the nodes as follows:7 - 11 - 2 - 4 - 5 - 13 - 8 - 4 - 1 where 7 is the 1st element in the tree, 11 is the 2nd element, etc.. For an ordered tree, the nodes will be in numerical order.
public int findK(int k) {
return findK(root, k);
}
private int findK(TreeNode current, int k) {
}
findKExtraCredit
This is for extra credit! A naive approach to finding the kth element in a tree would use an in-order traversal and return the kth element. However, this is in linear time and binary search trees should be able to access an element in O(treeHeight). In Compsci201 we care about efficiency so you will need to write the method in O(treeHeight).Hint: Modify your Node inner class to save the size of the subtree. That is, from the tree above, 5 would have a subtree size of 9, 4 would have a subtree size of 4, and 8 would have a subtree size of 4. Node 5 is the 5th node in the tree. This is one more than the size of its left subtree. You will need to check if the kth node is to the left or right of the current node you are on. You should then recurse on the appropriate subtree. Drawing pictures also helps.
public int findKExtraCredit(int k) {
return findK(root, k);
}
private int findKExtraCredit(TreeNode current, int k) {
}
