Recitation 8: Trees II

March 8, 2013

Submit your code, BST.java, to the Recitation 8 submit folder.

These questions use the TreeNode definition below and the following methods can be added to your BST code from March 1.

public class TreeNode { public int myValue; public TreeNode myLeft; // holds smaller tree nodes public TreeNode myRight; // holds larger tree nodes public int mySize; //the size of the subtree public TreeNode(int val) { myValue = val; } } By definition, the diameter of a tree (sometimes called the width) is the number of nodes on the longest path between two leaves in the tree. The diagram below shows two trees each with diameter nine, the leaves that form the ends of a longest path are shaded (note that there is more than one path in each tree of length nine, but no path longer than nine nodes).

It can be shown that the diameter of a tree T is the largest of the following quantities:

• the diameter of T's left subtree
• the diameter of T's right subtree
• the longest path between leaves that goes through the root of T (this can be computed from the heights of the subtrees of T)

Here's code that's almost a direct translation of the three properties above and the method height. The height of a tree is the length of the longest root-to-node path in the tree. For example, in the diagrams above the height of both trees is six.

public static int height(TreeNode t){ if (t == null) return 0; return 1 + Math.max(height(t.left), height(t.right)); } public static int diameter(TreeNode t) { if (t == null) return 0; int leftD = diameter(t.left); int rightD = diameter(t.right); int rootD = height(t.left) + height(t.right) + 1; return Math.max(rootD, Math.max(leftD, rightD)); }

After break we will talk about how to calculate the Big-Oh of recursive methods, however the method diameter as written above runs in greater than O(n) time.

1. We can write a version of diameter that runs in O(n) time. The recursion must return both the diameter and height of the left and right subtree in one call. To get two values we'll use an array in which the height is stored at index 0 and the diameter at index 1. A helper method is used as shown below. This method is O(n) because there is O(1) work done in addition to the two recursive calls. We will talk about this more after break.
   
   Complete diameterHelper so that it works as intended.
   /** * Return both height and diameter of t, return height as * value with index 0 and diameter as value with index 1 * in the returned array. * @param t is a binary tree * @return array containing both height (index 0) and diameter (index 1) */ public static int[] diameterHelper (TreeNode t) { int[] ret = new int[2]; // return this array if (t == null) { ret[0] = 0; // height is 0 ret[1] = 0; // and diameter is 0 return ret; } int[] left = diameterHelper(t.left); int[] right = diameterHelper(t.right); ret[0] = 1 + Math.max(left[0],right[0]); // this is height // fill in value for ret[1] below } public static int diameter(TreeNode t) { int[] ret = diameterHelper(t); return ret[1]; }
2. Two binary trees s and t are isomorphic if they have the same shape; the values stored in the nodes do not affect whether two trees are isomorphic. In the diagram below, the tree in the middle is not isomorphic to the other trees, but the tree on the right is isomorphic to the tree on the left.
   
   

   
   
   

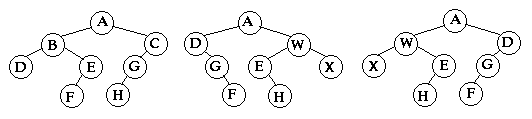
   Write a method isIsomorphic that returns true if its two tree parameters are isomorphic and false otherwise.

   Hint: a null trees is not isomorphic to a non-null tree, but two null trees are isomorphic. That's most-to-all of the base case you'll need. If the two trees have isomorphic left subtrees and isomorphic right subtrees, then they must be isomorphic.

   /** * Returns true if s and t are isomorphic, i.e., have same shape. * @param s is a binary tree (not necessarily a search tree) * @param t is a binary tree * @return true if and only if s and t are isomorphic */ public static boolean isIsomorphic(TreeNode s, TreeNode t) { }
3. Two trees s and t are quasi-isomorphic if s can be transformed into t by swapping left and right children of some of the nodes of s. The values in the nodes are not important in determining quasi-isomorphism, only the shape is important. The trees below are quasi-isomorphic because if the children of the nodes A, B, and G in the tree on the left are swapped, the tree on the right is obtained.

   

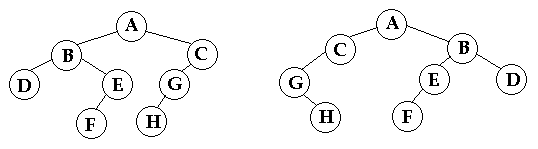
   Write a method isQuasiIsomorphic that returns true if two trees are quasi-isomorphic.

   The difference in quasi-isomorphism compared to isomorphism is that if the left subtree of one tree is quasi-isomorphic to the right subtree of the other, the trees might be quasi-isomorphic. Of course if the left subtrees are quasi-isomorphic the trees could be quasi-isomorphic as well.

   /** * Returns true if s and t are quasi-isomorphic, i.e., have same quasi-shape. * @param s is a binary tree (not necessarily a search tree) * @param t is a binary tree * @return true if and only if s and t are quasi-isomporphic */ public static boolean isQuasiIsomorphic(TreeNode s, TreeNode t) { }