Linear and Integer Programming (CPS 196/296.2), Spring 2008


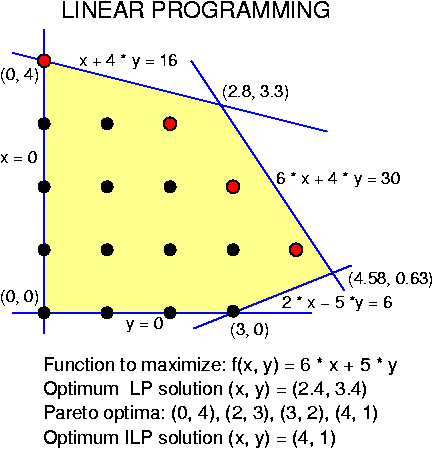
image taken from http://users.informatik.uni-halle.de/~jopsi/drand04/linear_programming.gif
Instructor: Vincent Conitzer.

Topics: Linear programming: applications, simplex method, duality theory, advanced techniques. Integer programming: applications, modeling, branch-and-bound, polyhedral theory, valid inequalities, advanced techniques.

Prerequisites: Linear algebra; probability; mathematical maturity (including ability to write a formal proof); basic computer science background or instructor's permission.

Summary:
In a linear program, we are given constraints of the form a_i1*x_1 + a_i2*x_2 + ... + a_in*x_n <= b_i, and we are asked to find the x_j that maximize an objective c_1*x_1 + c_2*x_2 + ... + c_n*x_n, subject to the constraints. In an integer (linear) program, the x_j must be integers. In a mixed integer (linear) program, only some of the x_j must be integers.

Surprisingly many optimization problems can be modeled as linear or integer programs. In this course, we will study how to model problems as linear or integer programs, and study basic methods (algorithms) for solving them.

Relevance to computer science theory and AI:
In spite of the strong algorithmic component of linear and integer programming, for historical reasons, much of the development of the techniques for these problems has taken place outside the computer science community. Because of this, computer scientists in general are perhaps less aware of them than they should be. Computer science theorists tend to be familiar at least with the techniques that allow for proving polynomial-time solvability, but are perhaps less interested in the (worst-case exponential-time) techniques for solving integer programs to optimality. Among AI researchers, the familiarity is perhaps even lower (with the exception of some subareas), even though they are generally not averse to algorithms that require exponential time in the worst case if they "usually" perform well. Indeed, many of the algorithms for integer programming are very similar to AI search algorithms.

Nevertheless, computer scientists (both in theory and AI) are increasingly looking at problems where these methods can be fruitfully applied. For example, the use of probabilities is becoming more common, which are continuous quantities that are naturally expressed in linear and integer programs. Moreover, both in theory and AI, there is increasing interest in problems from economics and game theory, which often lend themselves especially well to formulation as a linear or integer program.

Readings
I am making self-contained lecture notes for this course. Here are some (strictly optional) additional resources:
A course currently being taught at Harvard.
Applied Mathematical Programming, a book freely available online.

Grading
Participation: 10%
Homework: 20%
Midterm: 20%
Project: 50%
Bonus points: any mistakes/errors/typos that you (are the first to) find in my lecture notes (please send me e-mail with subject header "Mistake in notes").

You may discuss assignments with at most one other person. Each person must do her or his own writeup. Moreover, you may not simply write down a solution and give it to the other person. You may present things to each other on (say) a whiteboard, but the other person should not simply be copying things over. You should acknowledge everyone you worked with, as well as all other sources, on the writeup. Assignments are always due immediately at the beginning of class.

Projects
As you can see from the grading, the project is an important part of this course. You may work on it alone or in a team (please check with Vince first if you want to have a team of more than 3 people). I imagine that most projects will consist of using linear/integer programming in some application domain, perhaps in your own research area. Because of this, we will start discussing some example applications very early in the course, so that you can start thinking about how you might apply these techniques to something that you care about. We will have some checkpoints (e.g. project proposal) during the course, but feel free to discuss possible project ideas with Vince earlier.

The goal of the project is to try to do something novel, rather than merely a survey of existing work. Projects may be theoretical, experimental (based on simulations), experimental (based on real-world data), a useful software artifact, or any combination thereof. The only real constraint is that it has something to do with linear/integer programming. Talk to Vince if you are not sure about whether something is an appropriate project. The final product is a writeup (in the form of a research paper) and a class presentation (all team members must participate in the presentation). Some projects may well lead to publishable papers (perhaps with some additional work).

In your project proposal, you should explain the topic of your project, what types of results you hope to obtain, and what some of the technical issues are that you will need to address. If necessary, Vince can help with finding topics. Something related to your own research is definitely OK as long as it also has something to do with linear/integer programming. An intermediate project progress report is also required. This report should explain what results you have obtained already, what (if any) difficulties you encountered, and what you plan to do to complete your project. Ideally, at this point, you should already have some good results, so that you can spend the rest of your time on answering questions generated by your results, as well as preparing your writeup and presentation.

Dates:
Project proposal (1+ pages) due before class March 6.
Project progress report (~2 pages) due April 4.
Final project writeup due April 16 under my door.

Schedule
This is the first time I am teaching this course so we will be flexible with the schedule. One set of lecture notes will not necessarily take one lecture to finish.

Date	Topic	Materials
	Introduction. Examples of linear and integer programs. Solution by graphical inspection. Linear programs in abstract form.	Lecture notes 1.
	Applications. Maximum flow. Combinatorial (reverse) auctions. Zero-sum games. Markov decision processes. (Kemeny) rank aggregation. Sudoku.	Lecture notes 2.
	Using the GNU Linear Programming Kit and its modeling language.	Lecture notes 3. Homework 1.
	Duality. Weak duality, strong duality, complementary slackness.	Lecture notes 4.
	Duality in applications.	Lecture notes 5.
	A direct proof of strong duality.
	The simplex algorithm.	Lecture notes ?.
	Network flow problems.	Lecture notes ?.
	Constraint and column generation. The cutting stock problem.	Lecture notes ?.
	The ellipsoid algorithm. Polynomial-time separation oracles.	MIT lecture notes one and two. (For the midterm, you do not need to know things that we didn't cover in class.)
	An illustrative example: the core and network flows.	Lecture notes ?.
	Branch and bound.	Lecture notes ?.
	Valid inequalities/cutting planes.	Lecture notes ?.

---