
IWordOnBoardFinder ImplementationGoodWordOnBoardFinder correctly finds where a given word is
on the board.
You're given a JUnit test program TestWordFinder for
testing your word-finding code. Hopefully passing the unit tests will be
enough for your code to work in the Boggle game -- you can simply change
BoggleMain to use the
good word-finding implementation and the game should work properly.

cellsForWord which you must write
will call a recursive, helper method that does
most of the work. The helper method will search for the string/word
beginning at a specified (row,column) cell on the board -- the code in
method in cellsForWord calls the helper method with every
possible (row,column) as a starting point as follows:
public List<BoardCell> cellsForWord(BoggleBoard board, String word) {
List<BoardCell> list = new ArrayList<BoardCell>();
for(int r=0; r < board.size(); r++){
for(int c=0; c < board.size(); c++){
if (helper(board,r,c,list, ....)){
// not shown
You're free to write the helper method any way you want to, here's a suggestion.
The helper method can have an int parameter which is an
index indicating
which character in the string is the one being tentatively matched to
the (row,column) board cell. By convention, BoardCell indices
start with 0, where (0, 0) is the upper-left cell: The first time the helper method is called
this parameter has the value zero indicating the first character of the
string should be matched. There are several cases to track in the helper
method:
The helper method also maintains some record of the board cells that
have been matched so far. This record (could be a list or a set) serves
two purposes: it will ultimately be returned by the method
cellsForWord if the word is found on the board by the
helper method. The record will also help you write
code to ensure that the
same board cell isn't used more than once in finding the word being
searched for.
Although you can make eight recursive calls using eight different statements you can also use a loop like the one below to make the recursive calls:
int[] rdelta = {-1,-1,-1, 0, 0, 1, 1, 1};
int[] cdelta = {-1, 0, 1,-1, 1,-1, 0, 1};
for(int k=0; k < rdelta.length; k++){
if (helper(board, row+rdelta[k], col+cdelta[k], ...) return true;
}
Be careful when finding a "Q" in a word since if there's a match the Boggle board cube has two characters and you'll have to adjust parameters in the recursive call to make sure you do the right thing.
When you don't find the word being looked for, you'll have to backtrack
and undo the work done so far. As with typical, recursive,
backtracking
code, this often involves undoing the one step made before the recursive
invocation(s). In this case it's likely that the one-step-made is
storing
a matching BoardCell object.
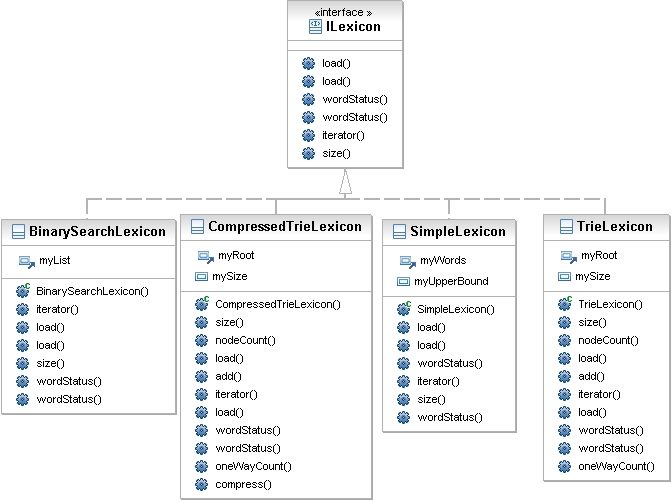
ILexicon Implementations
An inheritance diagram of the classes is given below -- the classes you
write must implement the methods of ILexicon and can
provide other methods as well if that helps in implementing the required
methods. Ignore the CompressedTrieLexicon class in the image below.
wordStatus methods of the
SimpleLexicon
class so that it uses the TreeSet.subSet method that returns a
subset/subtree of the tree in which all the words are stored --- the subset's
first word should be the String whose status is being determined in
wordStatus and the subset's last word should be
myUpperBound which is a value larger than any element in the
lexicon's set of words (see the code). Make sure you check to see if the
parameter s is larger than the upper bound since that will cause
the TreeSet.subset call to fail. See
the
SortedSet.subset API for details.
You must write a class named BinarySearchLexicon implementing the ILexicon interface. Store words in a sorted ArrayList (sort the
ArrayList after adding all the words to it) and use Collections.binarySearch to search the list.
Read the
documentation for binarySearch. Note
that when the index value returned is less than zero the value can be
used to determine where a word should be in a sorted list. For
example, when looking up "ela" the value returned might be
-137. This means that "ela" is not in the lexicon, but if it
were to be inserted it would be at index 136. This also means that if
the word at index 136 does not begin with "ela" then no word in
the lexicon has a prefix of "ela". So, any non-negative value returned
by binarySearch means the status of a word is
LexStatus.WORD. If the value returned is negative, one call
of the appropriate String.startsWith() method can determine
if LexStatus.PREFIX
should be returned (make sure you don't go off the
end of the array of words in the lexicon when calling
startsWith).
CompressedTrieLexicon,
but you may complete it for extra credit.
The compressed trie trades space for time. It is
slightly slower than a trie, but it requires less space/storage.
We provide a mostly complete TrieLexicon
implementation that we discussed in lab and which is explained in
some detail below. You'll also want to look at the code to understand
how the lexicon works. For extra credit you must implement a new
subclass of TrieLexicon; the subclass should
be named CompressedTrieLexicon. In implementing
the class you'll write code
to remove nodes with only one child as described below. A chain of nodes
pointed to by one link can be compressed into a node storing a
suffix rather than a single character. The picture below shows the
result of compressing such nodes in a trie.
You'll need to create a new method compress to perform this
one-child compression, you'll call this method in the load
method you override as below:
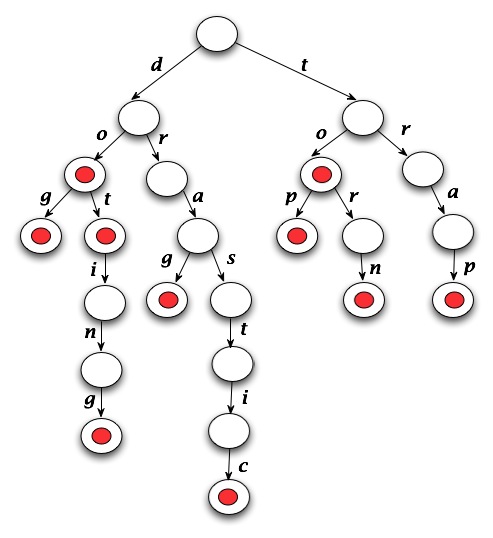
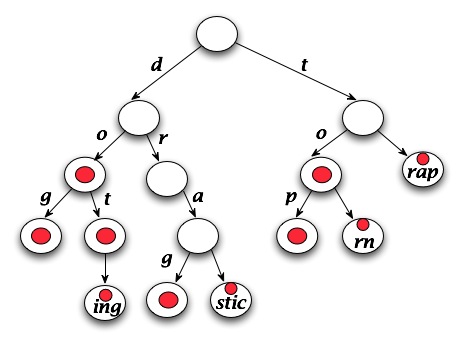
In a trie, determining whether a string is a word or a prefix is an O(W) operation where W is the length of the string -- note: this is independent of N the number of entries stored in the trie/lexicon. A picture of a trie storing the words "do", "dog", "dot", "doting", "drag", "drastic", "to", "top", "torn", and "trap" is shown below on the left. The compressed version of this trie is shown on the right.
| TrieLexicon | CompressedTrieLexicon |
|---|---|
|
|
The red dots in the diagram indicate that the path from the root to the
node represents a word. You can see how this works be examining the code
in the TrieLexicon
class. In particular, note that when a node has nothing below it, the
path to that node represents a word that isn't a prefix of another
word. Because of how the TrieLexicon is constructed,
determining if a sequence of characters is a word or a prefix is
fairly straightforward.
If a path hits a null pointerm then the path cannot represent either a prefix or a word since any pointer out of a node ultimately reaches a leaf that represents a word that isn't a prefix of another word. For example, in the tries shown above the string "toaster" would result in the code following the "t" link, then the "o" link from that, then would fail since there's no "a" link from the "o" node.
To compress the trie you'll write code that finds every leaf. From each leaf you'll write code that follows the parent pointers back up the trie until either a node representing a word is found or a node that has more than one child is found.
The second case is illustrated in the diagram by the strings "drastic", "torn", and "trap". In each case the sequence of nodes with single pointers is replaced by one node with a suffix stored that represents the eliminated nodes, e.g., "stic", "rn", and "rap" in the diagram. Note that the number of nodes eliminated is one less than the length of the suffix stored --- we need one node to store the suffix.
The first case described is represented by the string "doting". We can't replace "ting" by a node with that suffix because we'd have to differentiate between "dot" and "doting" and that's hard with one node. Instead we leave "dot" and only compress "ing" below it.
The suffix of the single-node-pointing-path is stored after the
parent pointers are followed. Since the trie nodes store a string, they
can certainly store a suffix. You'll need to code a new
version of wordStatus in the CompressedTrie
class to recognize when a suffix-node is reached.
You should benchmark your CompressedTrieLexicon class by
determining how many nodes are stored/saved compared to the
non-compressed trie and determining how much more time the new,
compressed version takes. Two methods in the
TrieLexicon class for counting nodes are provided,
they may prove useful in benchmarking your class. These
methods are nodeCount and oneWayCount.
TestLexicon to use as you develop
your ILexicon implementations. To test different implementations
simply change the code in the method makeLexicon to return the
implementation you want to test and run the JUnit tests (see the howto for JUnit assistance.)
We also provide a benchmarking class LexiconBenchmark that
facilitates evaluating the efficiency of different implementations as well as
correctness. Confidence in an implementation's correctness is increased if it
returns the same results as other implementations.
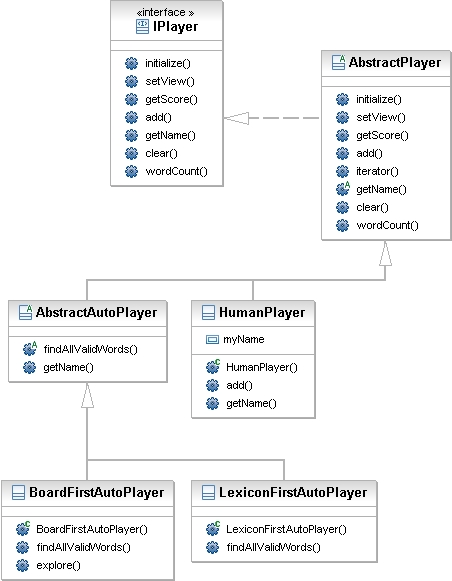
You'll write two classes that let the computer find all valid words on a
Boggle board. Each class will extend AbstractAutoPlayer and thus
implement the IAutoPlayer
interface. When you implement method
Here's a diagram of some of the classes and interfaces in the player
hierarchy. You'll implement the two classes at the bottom of the
diagram:
Once you've implemented
Rather than iterating over every every word in the dictionary you
can use the board to generate potential words. For example, in the
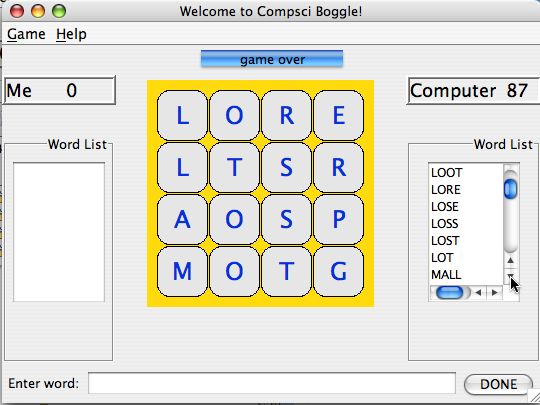
board shown in the screen shot below on the right the following words
can be formed starting the "L" in the upper-left corner:
"LORE", "LOSE", "LOST", "LOT". From the output it's clear that
"LOSER" isn't in the lexicon being used when the screen shot
was taken since it is on the board, but isn't shown
in the output.
Starting at the cell "R" at [1,3] (recall the
first row has index zero) we can form
"REST" and "RESORT". Starting
at the cell "R" at [0,2] we can
form "ROLL" and "ROSE" as well as "REST".
Since no word begins with "GT", "GP", "GS",
no search will proceed from the "G" in the lower-right
after looking at more than two cubes since these
two-character prefixes aren't found in the lexicon.
You'll write a recursive helper method for this class
to find all the words starting at a specified [row,column].
The basic idea is to pass to this helper method at least the
following:
The code you write will be very similar to the code you wrote
in
When first called, the string built from the search so far is the empty
string: "". The current cube/cell on the board, if legal and not used in
the search so far, is added to the end of the string built so far. If
the string is a word, the word is added to the collection of found words
by calling the inherited
As with all flood-fill/backtracking code you must make sure your code
doesn't re-use a board-cell/cube once it has been used in the current search. This
means that each board-cell/cube that contributed to the string built from the
search so far can't be re-used in extending the string. But the
cell/cube can be re-used when searching for different strings/starting
from or continuing from different cubes. You can use in instance
variable/field to store the
Boggle boards are generated by the BoggleBoardFactory class when its
You can ensure that some reproduceable sequence of boards is generated
by using
the
When debugging you may want to do this to ensure that you have
repeatable behavior. In your game-playing program you'll probably want
users to have a different sequence of boards every time, but in
debugging and statistic generation you want a reproduceable
sequence. For example, the supplied
Autoplayer Classes
findAllValidWords you
should first set the autoplayer's score to zero and then clear any words
already stored -- you do this by calling the inherited method
clear(). Remember that since you inherit all the classes
from AbstractAutoPlayer you can call them in the classes
you write. If you choose to override an inherited method you
should use the @Override annotation, but for the
auto-player classes you likely don't need to override any methods,
you simply need to implement findAllValidWords. You
may
find it useful to implement helper methods as well.
BoardFirstAutoPlayer and LexiconFirstAutoPlayer.
LexiconFirstAutoPlayer
GoodWordOnBoardFinder to find where
a word occurs on a board you'll be able write/implement class named
LexiconFirstAutoPlayer in a straightforward way. This new
class extends AbstractAutoPlayer. To find all the words on
a board simply iterate over every value in a lexicon checking to see if
the word is on the board by calling the cellsForWord method
you wrote earlier. This means you'll need to construct the
LexiconFirstAutoPlayer with an ILexicon and an
IWordOnBoardFinder to work with. These could be passed to
the constructor or could be fields that are initialized in the
constructor. For analyzing different lexicons you'll want to be able to
change which kind of ILexicon is used by the
LexiconFirstAutoPlayer, so parameterizing the constructor
makes some sense.
BoardFirstAutoPlayer
StringBuilder).
GoodWordOnBoardFinder.cellsForWord with its helper method.
add(..) method. (See the code in
AbstractPlayer for
how the words found are stored via this method.)
BoardCell objects used in the
current word being formed, but other approaches work as well (e.g.,
using a parameter) --- note that BoardCell implements
Comparable.
But, since you're backtracking, be sure to undo the
marking of a board cell both in the string being built and in the
structure storing which board cells contributed to the string.
Using JUnit
See the Markov Assignment Howto for information
on using JUnit.
Random Numbers
getBoard method is called. This method generates a board
by calling an IBoardMaker
implementation
makeBoard
method. You'll likely use the StandardBoardMaker
implementation supplied and created in the factory class.
This factory uses a random number generator without a specific
seed so that when you start a sequene of Boggle games different boards are
generated.
setRandom method of the
BoggleBoardFactory class
with a java.util.Random object created without a specific
seed, e.g.,
BoggleBoardFactory.setRandom(new Random(12345));
BoggleStats class sets the
seed to ensure that comparisons across different implementations of
lexicons and autoplayers are valid.
Last modified: Thu Mar 24 15:26:06 EDT 2011