See the How To pages for details on creating projects, files, and so on. The pages here describe in broad strokes what this assignment is about.
Genesis of the Markov Assignment

(image from Wikipedia, public domain)
This assignment has its roots in several places, with its modern description as the Infinite Monkey Theorem.
The true mathematical roots are from a 1948 monolog by Claude Shannon, A Mathematical Theory of Communication which discusses in detail the mathematics and intuition behind this assignment. This article was popularized by AK Dewdney in both Scientific American and later reprinted in his books that collected the articles he wrote.
Some examples of where Shannon’s mathematical theory have been applied include:
- In 2005 two students at MIT had a randomly-generated paper accepted at a conference. Their paper-generating tool, SCIgen, has a Wikipedia entry with links to the program.
- In 1984 an Internet Personality named Mark V Shaney participated in the then chat-room-of-the time using randomly generated text as described in this Wikipedia entry.
- In December 2008 Herbert Schlangemann had a auto-generated paper accepted and published in an IEEE “conference” (quotes used judiciously).
Joe Zachary developed this into a nifty assignment in 2003 and the folks at Princeton have been using this as the basis for an assignment since 2005 and possibly earlier.
More information on Markov models can be found here.
High Level View of Assignment
You’ll do three things for this assignment.
- Improve the performance of code that generates random text based on predicting characters. For this you’ll use a map to store information rather than (re)computing the information.
- Write a new random-text generation program based on words rather than characters.
- Modify, run, and report on a performance test comparing
HashMapandTreeMapimplementations of theMapinterface.
You’ll be provided with code that uses a brute-force approach to generate random text using an order-k Markov Model based on characters. You’ll first improve the code to make it more efficient, then you’ll write a new model based on words rather than on characters.
The term brute-force refers to the characteristic that the entire text that forms the basis of the Markov Model is rescanned to generate each letter of the random text.
For the first part of the assignment you’ll develop and use a Map (with other appropriate structures as keys and values) so that the text is scanned only once. When you scan once, your code will store information so that generating random text requires looking up information rather than rescanning the text.
Part 1: A Smarter Approach (for characters)
You will add a class, MapMarkovModel, based on the class MarkovModel that implements the following smarter approach for generating markov models. Make sure that you understand the brute-force method described here before trying to implement the smarter approach.
Instead of scanning the training text N times to generate N random characters, you’ll first scan the text once to create a structure representing every possible k-gram used in an order-k Markov Model. You may want to build this structure in its own method before generating your N random characters.
Example
Suppose the training text is "bbbabbabbbbaba" and we’re using an order-3 Markov Model.
The 3-letter string (3-gram) "bbb" occurs three times, twice followed by ‘a’ and once by ‘b’. We represent this by saying that the 3-gram "bbb" is followed twice by "bba" and once by "bbb". That is, the next 3-gram is formed by taking the last two characters of the seed 3-gram "bbb", which are "bb" and adding the letter that follows the original 3-gram seed.
The 3-letter string "bba" occurs three times, each time followed by ‘b’. The 3-letter string “bab”occurs three times, followed twice by ‘b’ and once by ‘a’. However, we treat the original string/training-text as circular, i.e., the end of the string is followed by the beginning of the string. This means "bab" also occurs at the end of the string (last two characters followed by the first character) again followed by ‘b’.
In processing the training text from left-to-right we see the following transitions between 3-grams starting with the left-most 3-gram "bbb"
bbb -> bba -> bab -> abb -> bba -> bab ->abb -> bbb ->bbb -> bba -> bab -> aba ->bab -> abb -> bbb
This can be represented as a map of each possible three grams to the three grams that follow it:
| 3-gram | following 3-grams |
|---|---|
| bbb | bba, bbb, bba |
| bba | bab, bab, bab |
| bab | abb, abb, aba, abb |
| abb | bba, bbb, bbb |
| aba | bab |
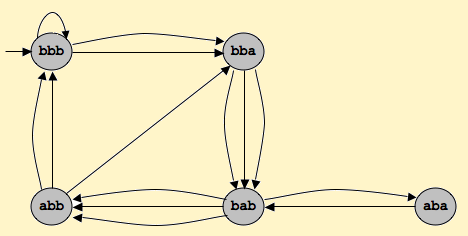
This information can also be represented in a state diagram (from the Princeton website).
Your Code
In your code you’ll replace the brute-force re-scanning algorithm for generating random text based on characters with code that builds a data structure that you’ll then use to follow the state transitions diagrammed above. Specifically, you’ll create a map to make the operation of creating random text more efficient.
Keys in the map are k-grams in a k-order Markov model. The value associated with each key is a list of related k-grams. Each different k-gram in the training text will be a key in the map. The value associated with a k-gram key is a list of every k-gram that follows key in the training text.
The list of k-grams that constitute a value should be in order of occurrence in the training text. That is, you should start generating your list of following grams from the beginning of your training text. See the table of 3-grams above as an example using the training text “bbbabbabbbbaba”. Note that the 3-gram key “bbb” would map to the list ["bba", "bbb", "bba"], the 3-gram key “bba”would map to the list ["bab", "bab", "bab"], and the 3-gram key “abb” would map to the list ["bba", "bbb", "bbb"]
Just like in the brute method, to generate random text your code should generate an initial seed k-gram at random from the training text, exactly as in the brute-force approach. Then use the pseudo-code outlined below.
seed = random k-character substring (k-gram) from the training text (key) --- the initial seed
repeat N times to generate N random letters
find the list (value) associated with seed (key) using the map
next-k-gram = choose a random k-gram from the list (value)
print or store C, the last character of next-k-gram
seed = next-k-gram // Note this is (last k-1 characters of seed) + C
Construct the map once — don’t construct the map each time the user tries to generate random text unless the value of k in the order-k Markov model has changed. See the howTo pages for details on the class you’ll implement and how it fits into the other classes.
Part 2: Markov Models for Words
In this part of the assignment you’ll use the character-generating Markov code you wrote as a model to create a new program that generates word models instead of character models. Your program will generate random words based on the preceding word k-grams. You’ll create a WordMarkovModel class that doesn’t use brute force. A helper class has been started for you, WordNgrams, where each WordNGram will be a word k-gram for your WordMarkovModel map. You will need to finish WordNGrams.
In the k-order Markov model with letters you just coded, k characters are used to predict/generate another character. In a k-order word Markov model k words are used to predict/generate another word — words replace characters. Here instead of a k-gram consisting of k letters, a WordNgram consists of k words. In your previous program you mapped every k-gram represented by a String to a list of following k-grams as Strings in this new program the key in the map will be a WordNgram representing every possible sequence of k-words. The associated value will be a list of the word k-grams that follow.
You need to write two classes:
- WordNgram: an object that represents N words from a text. This class has been started for you.
- WordMarkovModel: you need to write this class to generate a k-order Markov model random text
See the howTo pages for details.
Your WordNgram class must correctly and efficiently implement .equals, .hashCode, and .compareToso that WordNgram objects can be used in HashMap or TreeMap maps. Although you are not directly calling .equals, .hashCode, and .compareTo, these methods are needed by HashMap and TreeMap.
For full credit the hashCode value should be calculated once, not every time the method is called.
Document all .java files you write or modify. Submit all the .java files in your project. You should also submit a Analysis.pdf (described below) and README.
Part 3: Analysis
The analysis has 2 parts.
Part A
Answer these questions:
- How long does it take using the provided, brute force code to generate order-5 text using Romeo and Juliet (romeo.txt) and generating 100, 200, 400, 800, and 1600 random characters. Do these timings change substantially when using order-1 or order-10 Markov models? Why?
- Romeo has roughly 153,000 characters. Hawthorne’s Scarlet Letter contains roughly 500,000 characters. How long do you expect the brute force code to take to generate order-5 text when trained on hathorne.txt given the timings you observe for romeo when generating 400, 800, 1600 random characters? Do empirical results match what you think? How long do you think it will take to generate 1600 random characters using an order-5 Markov model when the King James Bible is used as the training text — our online copy of this text contains roughly 4.4 million characters. Justify your answer — don’t test empirically, use reasoning.
- Provide timings using your Map/Smart model for both creating the map and generating 200, 400, 800, and 1600 character random texts with an order-5 Model and romeo.txt. Provide some explanation for the timings you observe.
Part B
The goal of the second part of the analysis is to analyze the performance of WordMarkovModel using a HashMap (and the hashCode function you wrote) and a TreeMap (and the compareTo function you wrote). The main difference between them should be their performance as the number of keys (that is WordNGrams as keys in your map) gets large. So set up a test with the lexicons we give you and a few of your own. Figure out how many keys each different lexicon generates (for a specific number sized n-gram). Then generate some text and see how long it takes.
Graph the results. On one axis you’ll have the number of keys, on the other you’ll have the time it took to generate a constant of words (you decide…choose something pretty big to get more accurate results). Your two lines will be HashMap and TreeMap. Try to see if you can see any differences in their performance as the number of NGrams in the map get large. If you can’t, that’s fine. Briefly write up your analysis (like 1 or 2 paragraphs) and include both that and the graph in a PDF you submit.
Call the file Analysis.pdf so that our checking program can know that you submitted the right thing.
High-Level Grading
| Criteria | Points |
|---|---|
| Map-based Markov Model works and is more efficient than brute force code given | 5 |
| WordNGram Markov Model works and meets the requirements of hashCode and Comparable | 5 |
| Analysis | 5 |
More High-Level Grading
To get full credit on an assignment your code should be able to do the following.
- Create new classes without overwriting old classes.
- Don’t unnecessarily repeat expensive computations (making maps maybe?).
- Results should be consistent.
- Overwritten methods should operate correctly (equals, compareTo, etc).
- Answer write-up questions using full thoughts/sentences. Explain clearly or demonstrate with data.
- You *MUST* create and submit a README with your work.
- If you have questions about the assignment that are not specific to your code, please ask on Piazza and we will be happy to clarify. If your question is specific to the code you’ve written please post it privately on Piazza, or bring it to the Link or Office Hours and don’t share it directly with your classmates.
This list is not a complete rubric for grading, and there is a better breakdown on the main page. Please start early, work carefully, and ask any questions you have and we’ll do our best to make sure that everyone gets all of the points that they deserve.