Find Words on the Board
You’re given a class BadWordOnBoardFinder that implements the IWordOnBoardFinder interface. The bad word finder returns an empty list of BoardCell objects for any query so no words will be found. In other words it fails to correctly find any words.
You’ll implement the method cellsForWord in a class GoodWordOnBoardFinder using a standard, backtracking search to find a word on a Boggle board. This is desccribed below.
A Good IWordOnBoardFinder Implementation
The screen show below shows a game in which the word “mountain” is highlighted on the board — the highlighting is done because a class GoodWordOnBoardFinder correctly finds where a given word is on the board.
You’re given a JUnit test program TestWordFinder for testing your word-finding code. Hopefully passing the unit tests will be enough for your code to work in the Boggle game — you can simply change BoggleMain to use the good wordfinding implementation and the game should work properly.

Backtracking Code
To find whether a String/word occurs on a board the method cellsForWord which you must write will call a recursive, helper method that does most of the work. The helper method will search for the string/word beginning at a specified (row,column) cell on the board — the code in method incellsForWord calls the helper method with every possible (row,column) as a starting point as follows:
public List<BoardCell> cellsForWord(BoggleBoard board, String word) {
List<BoardCell> list = new ArrayList<BoardCell>();
for(int r=0; r < board.size(); r++){
for(int c=0; c < board.size(); c++){
if (helper(board,r,c,list, ....)){
// not shown
You’re free to write the helper method any way you want to, here’s a suggestion.
The helper method can have an int parameter which is an index indicating which character in the string is the one being tentatively matched to the (row,column) board cell. The first time the helper method is called this parameter has the value zero indicating the first character of the string should be matched. There are several cases to track in the helper method:
- If the index of the string is too large, the word has been found since no more letters are left to find on the board.
- If the row and column are out of bounds, don’t continue the search
- If the specified character in the string matches the character in the (row,column) board cell then up to eight recursive calls will be made to find the next letter in the string (changed parameter in recursive call) in a neighboring cell (changed parameter in recursive call).
- Be sure not to re-use a previously used board cell.
- When things work, watch out for “Qu”, the tricky Q-cube.
The helper method also maintains some record of the board cells that have been matched so far — this record is maintained in a parameter that is passed in each recursive calls. This record, which is likely a list or a set, serves two purposes: it will ultimately be used to return something by the method cellsForWord if the word is found on the board by the helper method. The record will also help you write code to ensure that the same board cell isn’t used more than once in finding the word being searched for (e.g., you can use the method .contains to see if a BoardCellhas been used before).
Although you can make eight recursive calls using eight different statements you can also use a loop like the one below to make the recursive calls.
int[] rdelta = {-1,-1,-1, 0, 0, 1, 1, 1};
int[] cdelta = {-1, 0, 1,-1, 1,-1, 0, 1};
for(int k=0; k < rdelta.length; k++){
if (helper(board, row+rdelta[k], col+cdelta[k], ...)
return true;
}
Be careful when finding a “Q” in a word since if there’s a match the Boggle board cube has two characters and you’ll have to adjust parameters in the recursive call to make sure you do the right thing.
When you don’t find the word being looked for, you’ll have to backtrack and undo the work done so far. As with typical, recursive, backtracking code, this often involves undoing the one step made before the recursive invocation(s). In this case it’s likely that the one-step-made is storing a matching BoardCell object.
Different ILexicon Implementations
Details about the classes you write for this part of the assignment and help in writing them are provided below.
You’ll design and code one class for this part of the assignment and you’ll analyze the performance of several classes empirically. There is a Lexicon you can implement for extra credit as well. You’re given a JUnit testing class, TestLexicon, to test your implementations — see the JUnit Section for help/reminders on using JUnit. In the ILexicon.load methods you write you can assume no duplicate words will be inserted via either the Scanner or ArrayList parameters to the load methods. You’re also given a class LexiconBenchmark you can use to analyze the empirical performance of your implementations.
In Boggle®, legal words are those found in the lexicon associated with a game. A lexicon is simply a list of words, it’s not a dictionary because it doesn’t have associated definitions for each word.
The ILexicon interface specifies the methods which implementations must provide. You’re given an implementation SimpleLexicon with an O(n) implementation of the method wordStatus since the implementation simply does a linear search over the list of words it stores. Read thedocumentation for details of the interface.
An inheritance diagram of the classes is given below — the classes you write must implement the methods of ILexicon and can provide other methods as well if that helps in implementing the required methods.
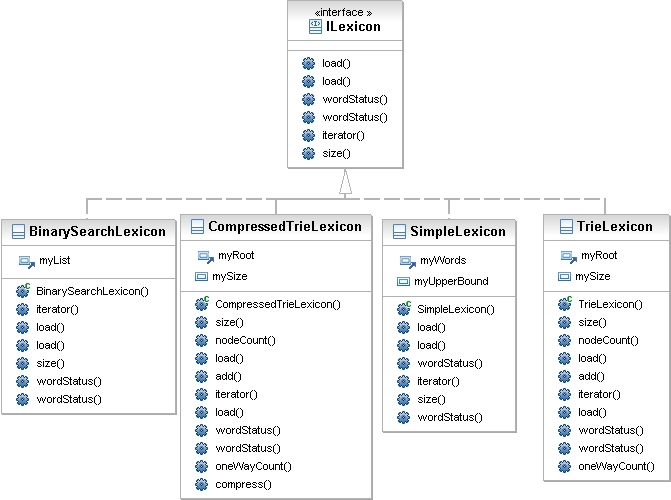
SimpleLexicon
This code is written for you – just use it in your analysis.
BinarySearchLexicon
You must modify the class named BinarySearchLexicon implementing the ILexicon interface. The existing code stores words in a ArrayList. You’ll need to modify the code to sort in method.wordStatus to use Collections.binarySearch to search the list.
Read the documentation for binarySearch. Note that when the index value returned is less than zero the value can be used to determine where a word should be in a sorted list. For example, when looking up “ela” the value returned might be -137. This means that “ela” is not in the lexicon, but if it were to be inserted it would be at index 136. This also means that if the word at index 136 does not begin with “ela” then no word in the lexicon has a prefix of “ela”. So, any non-negative value returned by binarySearch means the status of a word is LexStatus.WORD. If the value returned is negative, one call of the appropriate String.startsWith() method can determine if LexStatus.PREFIX should be returned (make sure you don’t go off the end of the array of words in the lexicon when calling startsWith).
CompressedTrieLexicon
For extra credit you must implement a lexicon based on a compressed trie data structure. The compressed trie trades space for time: it is slightly slower than a trie, but it requires less space/storage.
We provide the TrieLexicon implementation that we’ll discuss in class and which is explained in some detail below. You’ll also want to look at the code to understand how the lexicon works. For extra credit you must implement a new subclass of TrieLexicon; the subclass should be namedCompressedTrieLexicon. In implementing the class you’ll write code to remove nodes with only one child as described below. A chain of nodes pointed to by one link can be compressed into a node storing a suffix rather than a single character. The picture below shows the result of compressing such nodes in a trie.
You’ll need to create a new method compress to perform this one-child compression, you’ll call this method in the load method you override as below:
public class CompressedTrieLexicon extends TrieLexicon {
// some code not shown
@Override
public void load(ArrayList<String> list) {
super.load(list);
compress();
}
// more code not shown
}
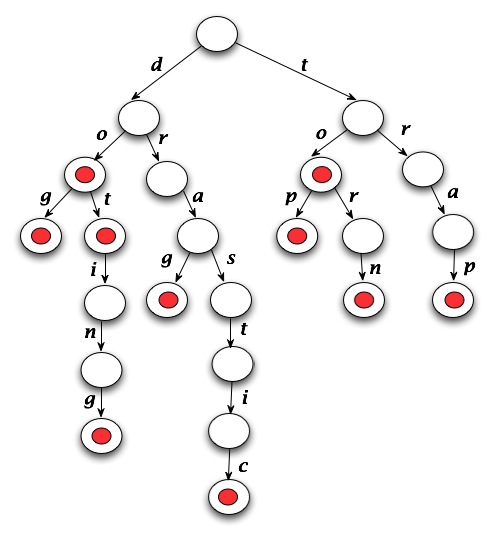
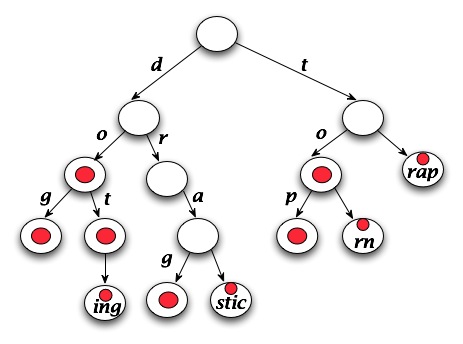
In a trie, determining whether a string is a word or a prefix is an O(W) operation where W is the length of the string — note: this is independent of N the number of entries stored in the trie/lexicon. A picture of a trie storing the words “do”, “dog”, “dot”, “doting”, “drag”, “drastic”, “to”, “top”, “torn”, and “trap” is shown below on the left. The compressed version of this trie is shown on the right.
| TrieLexicon | CompressedTrieLexicon |
|---|---|
 |
 |
The red dots in the diagram indicate that the path from the root to the node represents a word. You can see how this works be examining the code in the TrieLexicon class. In particular, note that when a node has nothing below it, the path to that node represents a word that isn’t a prefix of another word. Because of how the TrieLexicon is constructed, determining if a sequence of characters is a word or a prefix is fairly straightforward as shown below.
public LexStatus wordStatus(StringBuilder s){
Node t = myRoot;
for (int k = 0; k < s.length(); k++) {
char ch = s.charAt(k);
t = t.children.get(ch);
if (t == null)
return LexStatus.NOT_WORD; // no path below? done
}
return t.isWord ? LexStatus.WORD : LexStatus.PREFIX;
}
Note that if the path hits a null pointer the path cannot represent either a prefix or a word since any pointer out of a node ultimately reaches a leaf that represents a word that isn’t a prefix of another word.
For example, in the tries shown above the string “toaster” would result in the code following the “t” link, then the “o” link from that, then would fail since there’s no “a” link from the “o” node.
To compress the trie you’ll write code that finds every leaf. From each leaf you’ll write code that follows the parent pointers back up the trie until either a node representing a word is found or a node that has more than one child is found.
The second case is illustrated in the diagram by the strings “drastic”, “torn”, and “trap”. In each case the sequence of nodes with single pointers is replaced by one node with a suffix stored that represents the eliminated nodes, e.g., “stic”, “rn”, and “rap” in the diagram. Note that the number of nodes eliminated is one less than the length of the suffix stored — we need one node to store the suffix.
The first case described is represented by the string “doting”. We can’t replace “ting” by a node with that suffix because we’d have to differentiate between “dot” and “doting” and that’s hard with one node. Instead we leave “dot” and only compress “ing” below it.
The suffix of the single-node-pointing-path is stored after the parent pointers are followed. Since the trie nodes store a string, they can certainly store a suffix. You’ll need to code a new version ofwordStatus in the CompressedTrie class to recognize when a suffix-node is reached.
You should benchmark your CompressedTrieLexicon class by determining how many nodes are stored/saved compared to the non-compressed trie and determining how much more time the new, compressed version takes. Two methods in the TrieLexicon class for counting nodes are provided, they may prove useful in benchmarking your class. These methods are nodeCount andoneWayCount.
Lexicon Testing and Benchmarking
We provide a JUnit testing class TestLexicon to use as you develop your ILexicon implementations. To test different implementations simply change the code in the method makeLexicon to return the implementation you want to test and run the JUnit tests (see the howto for JUnit assistance.)
We also provide a benchmarking class LexiconBenchmark that facilitates evaluating the efficiency of different implementations as well as correctness. Confidence in an implementation’s correctness is increased if it returns the same results as other implementations.
Autoplayer Classes
Details about the classes you write for this part of the assignment and help in writing them are provided below.
You’re given one class LexiconFirstAutoPlayer and you’ll implement a new AutoPlayer that finds all the words on a Boggle board. Each class uses a different technique and you’ll analyze the runtime tradeoffs in these techniques. You’ll also reason empirically about the performance of these two classes when they’re configured with different implementations of ILexicon lexicons.
One class, BoardFirstAutoPlayer looks at the board and tries to form words by trying all the paths on the board. The code will be very similar to the backtracking code you wrote for theGoodWordOnBoardFinder class, but you’ll prune searches early based on prefixes as described below. You’re given another class, LexiconFirstAutoPlayer, that is relatively simple to implement since you’ll have working lexicons and a working WordOnBoardFinder from earlier in this assignment. In implementing the LexiconFirstAutoPlayer code looks up every word in the lexicon to see if it’s on the board. This method is surprisingly fast enough for a game of Boggle , but it’s probably not fast enough to run 10,000 times without waiting for a while.
Each class extends AbstractAutoPlayer and thus implements the IAutoPlayer interface. When you implement method findAllValidWords you should first set the autoplayer’s score to zero and then clear any words already stored (see the code you’re given in LexiconFirstAutoPlayer – you do this by calling the inherited method clear(). Remember that since you inherit all the methods fromAbstractAutoPlayer you can call them in the subclasses you write. If you choose to override an inherited method you should use the @Override annotation, but for the auto-player classes you likely don’t need to override any methods, you simply need to implement findAllValidWords. You may find it useful to implement helper methods as well.
Here’s a diagram of some of the classes and interfaces in the player hierarchy. You’ll implement the two classes at the bottom of the diagram: BoardFirstAutoPlayer and LexiconFirstAutoPlayer.
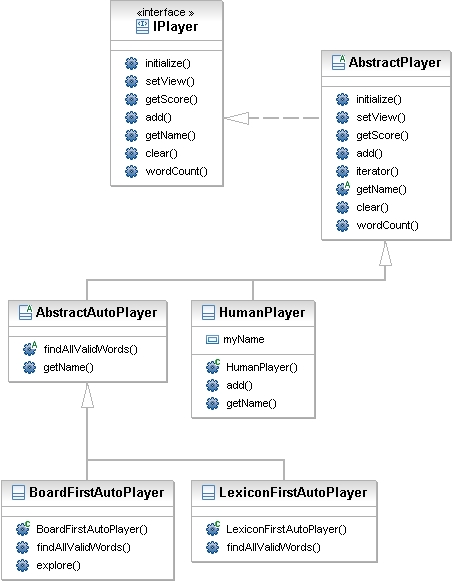
LexiconFirstAutoPlayer
Once you’ve implementedGoodWordOnBoardFinder to find where a word occurs on a board you’ll be able to write/implement (complete) the class LexiconFirstAutoPlayer. This new class extendsAbstractAutoPlayer. To find all the words on a board simply iterate over every value in a lexicon checking to see if the word is on the board by calling the cellsForWord method you wrote earlier.
The code to do this is already written for you – just change LexiconFirstAutoPlayer to use theGoodWordOnBoardFinder you wrote.
BoardFirstAutoPlayer
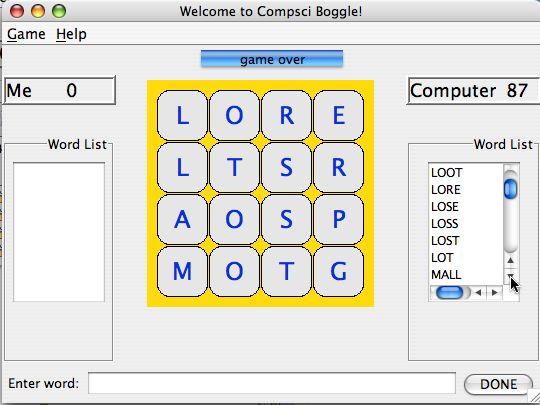
Rather than iterating over every every word in the dictionary you can use the board to generate potential words. For example, in the board shown in the screen shot below on the right the following words can be formed starting the “L” in the upper-left corner: “LORE”, “LOSE”, “LOST”, “LOT”. From the output it’s clear that “LOSER” isn’t in the lexicon being used when the screen shot was taken since it is on the board, but isn’t shown in the output.
Starting at the cell “R” at [1,3] (recall the first row has index zero) we can form “REST” and “RESORT”. Starting at the cell “R” at [0,2] we can form “ROLL” and “ROSE” as well as “REST”.
Since no word begins with “GT”, “GP”, “GS”, no search will proceed from the “G” in the lower-right after looking at more than two cubes since these two-character prefixes aren’t found in the lexicon.
You’ll write a recursive helper method for this class to find all the words starting at a specified [row,column]. The basic idea is to pass to this helper method at least the following:
- The current row, column.
- The string built from the search so far (you may want to use a
StringBuilder).
The code you write will be very similar to the code you wrote inGoodWordOnBoardFinder.cellsForWord with its helper method.
When first called, the string built from the search so far is the empty string: “”. The current cube/cell on the board, if legal and not used in the search so far, is added to the end of the string built so far. If the string is a word, the word is added to the collection of found words by calling the inherited add(..) method. (See the code in AbstractPlayer for how the words found are stored via this method.)
If the string is either a word or the prefix of a word in the lexicon then the search is continued by calling the helper method for each adjacent cube with the string built so far. If the string is not a prefix (or a word) then the search is cut-off at this point and the recursion will unwind/backtrack (essentially to the point where the last possible word/prefix was formed).As with all flood-fill/backtracking code you must make sure your code doesn’t re-use a board-cell/cube once it has been used in the current search. This means that each board-cell/cube that contributed to the string built from the search so far can’t be re-used in extending the string. But the cell/cube can be re-used when searching for different strings/starting from or continuing from different cubes. You can use in instance variable/field to store the BoardCell objects used in the current word being formed, but other approaches work as well (e.g., using a parameter) — note that BoardCell implements Comparable. But, since you’re backtracking, be sure to undo the marking of a board cell both in the string being built and in the structure storing which board cells contributed to the string.
Using JUnit
See the Markov Assignment Howto or the DNA Assignment Howto for information on using JUnit. For testing Lexicons you’ll need to modify the method .makeLexicon in TestLexicon.java and run JUnit tests. To test GoodWordOnBoardFinder change the method TestWordFinder.setUp. n
BoggleStats and Random Numbers
Boggle boards are generated by the BoggleBoardFactory class when its getBoard method is called. This method generates a board by calling an IBoardMaker implementation makeBoard method. You’ll likely use the StandardBoardMaker implementation supplied and created in the factory class. This factory uses a random number generator without a specific seed so that when you start a sequene of Boggle games different boards are generated.
You can ensure that some reproduceable sequence of boards is generated by using the setRandommethod of the BoggleBoardFactory class with a java.util.Random object created with a specific seed, e.g.,
BoggleBoardFactory.setRandom(new Random(12345));
When debugging you may want to do this to ensure that you have repeatable behavior. In your game-playing program you’ll probably want users to have a different sequence of boards every time, but in debugging and statistic generation you want a reproduceable sequence. For example, the supplied BoggleStats class sets the seed to ensure that comparisons across different implementations of lexicons and autoplayers are valid.
Statistical and Empirical Analyses of Boggle
You need to report in your Analysis file information about which Lexicon implementation is fastest. You should compare all the lexicons and report on their relative times — you shouldn’t simply say “this one is fastest”. You should have at least three lexicons to test and four if you do the extra credit. You should explain the methods you used to determine this and report on experiments you run, giving times.
You must write code to play lots of auto-games, not games in which humans play, but games in which all words are found on thousands of boards — see BoggleStats for a starting point. You must provide a board that scores the highest of all the 4×4 and 5×5 boards you test in running at least 10,000 auto-games. and preferably 50,000 games. Report on how many seconds it takes your code to run for 1,000 games; for 10,000 games (or predict that if you can’t run that many); and predict/justify on how much time it would take your computer and implementation to simulate both 100,000 games and one million games. When doing the experiments be sure to set the random-number generator’s seed, currently done already in BoggleStats and described above. If you can’t run 10,000 auto-games, indicate the maximum number you can run.